Задание множества осуществляется либо
1) перечислением элементов, например, А = {1, 2, 3},
2) либо с помощью характеристического свойства, т.е. свойства, которым обладает каждый элемент множества и не обладают никакие другие, например, В = { х: 1< х < 3},
 3) либо с помощью графического изображения (геометрические фигуры на плоскости) – кругов Эйлера:
3) либо с помощью графического изображения (геометрические фигуры на плоскости) – кругов Эйлера:
Иногда характеристическим свойством не обладает ни один объект множества, что повлекло за собой введение понятия пустого множества.
Определение 3. Множество, не имеющее ни одного элемента, называется пустым 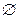 .
.
Определение 4. Множества А и В называются равными, если состоят из одних и тех же элементов: А = В. В противном случае 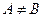 .
.
Символ «=» равенства множеств обладает свойствами: а) Х = Х – рефлексивность, б) если Х = Y, то У = Х – симметричность, в) если Х = У и У = Z, то Х = Z – транзитивность.
Из определения 4 вытекает, что порядок элементов в множестве не существенен. Например, А = {1, 2, 3, 4} и В = {4, 1, 3, 2} – одно и то же множество.
Из определения множества следует, что в нем не должно быть неразличимых элементов, поэтому в множестве не может быть одинаковых элементов. Запись {1, 1, 2, 3} следует рассматривать как некорректную и заменять на {1, 2, 3}.
Определение 5. Символ 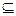 – отношение включения множеств, т.е. если
– отношение включения множеств, т.е. если 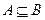 (А включено в В), то каждый элемент множества А является элементом множества В. При этом множество А называется подмножеством, множество В – надмножеством. Если
(А включено в В), то каждый элемент множества А является элементом множества В. При этом множество А называется подмножеством, множество В – надмножеством. Если 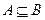 и
и 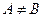 , то А называется собственным подмножеством В. В этом случае пишут
, то А называется собственным подмножеством В. В этом случае пишут 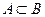 .
.
Пустое множество 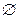 – подмножество любого множества.
– подмножество любого множества.
 2015-05-22
2015-05-22 820
820








