2015-05-22
2145
Пусть А, В, С – произвольные подмножества множества F. Тогда непосредственно из определений объединения, пересечения и дополнения вытекают следующие законы:
1. 
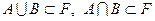– замкнутость операций объединения и пересечения,
2. 
, 
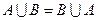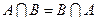– коммутативность операций объединения и пересечения,
3. 
– ассоциативность операции объединения,
4. 
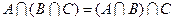– ассоциативность операции пересечения,
5. 
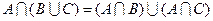– дистрибутивность операции пересечения относительно операции объединения,
6. 
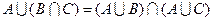– дистрибутивность операции объединения относительно операции пересечения,
7. 
,
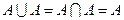8. 
,
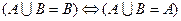9. 
,
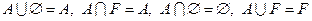10. 
,
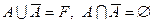11. 
, 
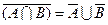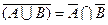– законы де Моргана.
Определение 12. Если для элементов множества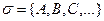 
определены операции объединения 
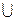и пересечения 
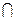, для которых выполняются данные законы, то тройка 
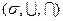называется булевой алгеброй. Таким образом, если 
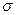– семейство всех частей множества F, то 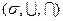– булева алгебра.
Отличие алгебры чисел от алгебры множеств:
Если а и b – два числа, то между ними может быть три соотношения: a > b, a < b, a = b. Для двух множеств А и В может не выполняться ни одно из соотношений: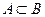 
, 
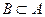, А = В.
|
|
|
