Решение. Возможные значения случайной величины m: 0,1,2,3,4

1) n = 4, p = 0,8.

Возможные значения случайной величины m: 0,1,2,3,4. Пусть им соответствуют вероятности Р ₀, Р ₁, Р ₂, Р ₃, Р ₄. Найдём их, используя формулу Бернулли: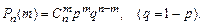

, ,

, ,

.

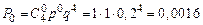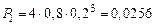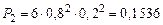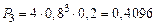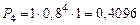Таким образом ряд распределения имеет следующий вид:

m
р	0,0016	0,0256	0,1536	0,4096	0,4096

По определению функция распределения находится по формуле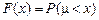

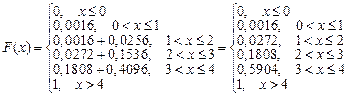
Найдём М (m):

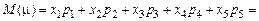
= 0 × 0,0016 + 1 × 0,0256 + 2 × 0,1536 + 3 × 0,4096 + 4 × 0,4096 = 3,2.

Дисперсию будем искать по формуле .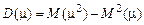

Составим закон распределения для x².

x2
р	0,0016	0,0256	0,1536	0,4096	0,4096

М (m²) = 0,0256 + 4 ×0,1536 + 9 × 0,4096 + 16 × 0,4096 = 10,88.

D (x) = 10,88 – (3,2)² = 0,64.

По функции распределения Р (m £ 2) = F (3) = 0,1808.

2) n = 1000, p = 0,004.

Р (m £ 2) = Р (m = 0) + Р (m = 1) + Р (m = 2). По формуле Пуассона 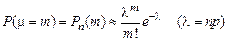. Таким образом, имеем: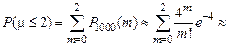

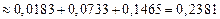
(значения P_n (m) найдены по таблице).

3) n = 100, p = 0,8, m ₁ = 75, m ₂ = 90.

По условию задачи q = 1– p = 0,2.

Воспользуемся интегральной теоремой Лапласа:

P_n (k ₁ £ k £ k ₂) = F(x ₂) – F(x ₁), где F(x) – функция Лапласа,

, .

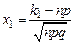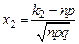Вычислим x ₁ и x ₂:

,

.

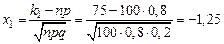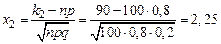Так как функция Лапласа нечетна, т.е. F(– x) = –F(x), получим

P ₁₀₀(75 £ k £ 90) = F(2,25) – F(–1,25) = F(2,25) + F(1,25).

По таблице значений функции Ф найдем:

F(2,25) = 0,4938; F(1,25) = 0,3944.

Искомая вероятность

P ₁₀₀(75 £ k £ 90) = 0,4938 + 0,3944 = 0,8882.

ЗАДАЧА. Дана функция плотности распределения

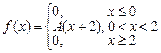
Найти: 1) параметр А; 2) построить графики плотности и функции распределения; 3) Р(1<x<4); 4) М (Х), D (X), s(X); 5) верятность Р, что отклонение случайной величины от М (Х) не более 1.

РЕШЕНИЕ. Так как 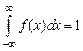, получаем 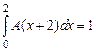, так как 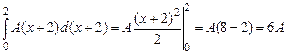, тогда .

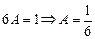Итак,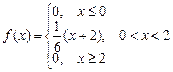

Найдём F (х), функцию распределения по формуле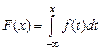

если ,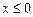

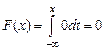
если ,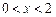

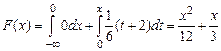
если ,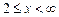

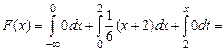
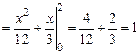
Итак,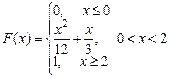

Построим оба графика

Найдём P (1 < x < 4).

Так как P (х ₁ < x < х ₂) = F (х ₂) – F (х ₁)

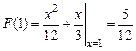, F (4) = 1,

P (1 < x < 4) = 1– .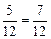

Найдём М (X) по формуле .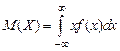

.

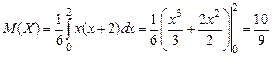Дисперсия вычисляется по формуле

.

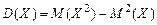
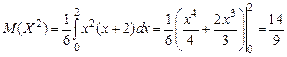
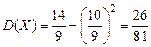Среднее квадратическое отклонение .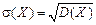

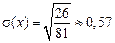
Найдём 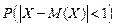. Так как, 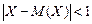, следует 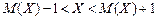в нашей задаче 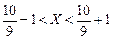или 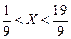, то необходимо найти

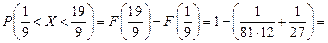
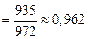
ЗАДАЧА. Масса вагона - случайная величина, распределённая по нормальному закону с математическим ожиданием 65 т и средним квадратичным отклонением 0,9 т. Найти вероятность того, что вагон имеет массу не более 67 т и не менее 64 т. По правилу трёх сигм найти наибольшую и наименьшую границы предполагаемой массы.

РЕШЕНИЕ. Для нормального распределённой случайной величины

.

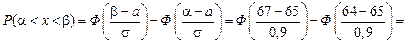
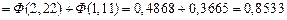По правилу трёх сигм наименьшая граница 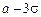, наибольшая граница 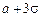. Таким образом,

.

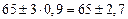Наименьшая граница 62,3 т, наибольшая 67,7 т.

ЗАДАЧА. В двух ящиках находятся по шесть шаров; в 1-м ящике: 1 шар – с №1, 2 шара – с №2, 3 шара – с №3; во 2-м ящике: 2 шара с №1, 3 шара с №2, 1 шар – с №3. Пусть Х – номер шара, вынутого из первого ящика, Y – номер шара, вынутого из второго ящика. Из каждого ящика вынули по шару. Составить таблицу закона распределения системы случайных величин (X, Y). Найти математические ожидания и дисперсии случайных величин X и Y. Определить коэффициент корреляции.