Условным законом распределения одной случайной величины,входящей в систему, называется закон, найденный при условии, что другая случайная величина, входящая в эту же систему, приняла определенное значение. Условный закон распределения задается как функцией распределения, так и плотностью распределения. Если рассматривается распределение случайной величины ξi при условии, что другая случайная величина ξj приняла определенное значение, то условная функция распределения обозначается
F(x/y), а плотность – f(x/ y).
Важными характеристиками являются условные математические ожидания и условные дисперсии. Пусть случайная величина ξi принимаетзначения
a = (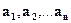 ), а случайная величина ξj - b = (
), а случайная величина ξj - b = (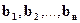 ).
).
Условным математическим ожиданием дискретнойслучайной величины ξi при ξj = bназывают сумму произведений возможных значений ξ i на их условные вероятности. Тогда условное математическое ожидание вычисляется по формуле:
M(ξi / ξj=b) = 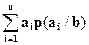 . (27)
. (27)
Для непрерывных случайных величин
M(ξi / ξj=b) = 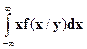 . (28)
. (28)
Особая роль в изучении системы случайных величин принадлежит корреляционному моменту (ковариации). Ковариацией случайных величин ξ i и ξj называется число
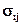 = cov(ξiξj) = M((ξ i-M(ξ i))(ξ j-M(ξj)))=M(ξiξj)-M(ξi)M(ξj), i,j=1,2,…n.
= cov(ξiξj) = M((ξ i-M(ξ i))(ξ j-M(ξj)))=M(ξiξj)-M(ξi)M(ξj), i,j=1,2,…n.
Для независимых случайных величин ковариация равна нулю т.к. в этом случае M(ξiξj) = M(ξi)M(ξj).
Очевидно, что 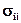 =
= 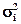 = D(
= D(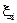 ), cov(ξiξ j) = cov(ξ
), cov(ξiξ j) = cov(ξ 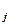 ξ
ξ 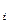 )
)
Все парные ковариации составляют симметричную относительно главной диагонали ковариационную матрицу размерностью (n 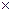 n).
n).
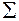 =
= 
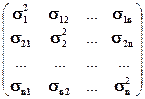
Определитель ковариационной матрицы является обобщенной дисперсией системы случайных величин..
Рассмотрим систему только двух случайных величин, пусть ξ1, ξ2. Пусть случайная величина ξ1 принимает значения из множества X, ξ2 – из множества Y, (X,Y) -действительные числа. Мерой линейной зависимости двух случайных величин ξ1, ξ2 является коэффициент корреляции
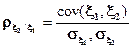 ,
,
Свойства коэффициента корреляции:
1. |ρ| 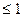 .
.
2. |ρ|=1 тогда и только тогда, когда между случайными величинами существует
линейная функциональная взаимосвязь
y = аx + b, (29)
где 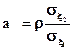
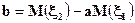 ,
,
причем, если ρ= 1, то a > 0, если ρ= -1, то a < 0 (Рис. 15)
 |
Рис. 15.
Для независимых случайных величин ρ = 0, но обратное утверждение неверно, т.к. между случайными величинами может быть другой тип взаимосвязи (нелинейной).Чем ближе значение ρ к нулю, тем слабее линейная взаимосвязь, чем ближе по модулю к единице, тем -сильнее. Если ρ = 0, то говорят, что случайные величины некоррелированы. Можно показать, что если нормально распределенные случайные величины некоррелированы, то они и независимы.
Пусть –1<ρ<1 и ρ≠0. Если нанести точки (X,Y) на координатную плоскость XoY, то можно заметить, что эти точки группируются вокруг некоторой прямой y = ax + b. Вычислим коэффициенты a,b этой прямой из условия, что дисперсия 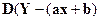 отклонений точек (X,Y) от точек на прямой была минимальна.
отклонений точек (X,Y) от точек на прямой была минимальна.

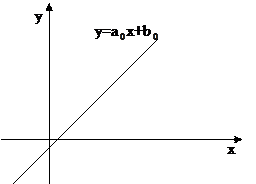 .
.
.
.
.
.
Рис. 16.
Уравнение, относительно которого дисперсия минимальна, называется уравнением регрессии. Рассматривая дисперсию как функцию от двух переменных a и b воспользуемся необходимым условием экстремума
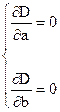
Решая эту систему относительно a и b, получим
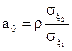 ,
, 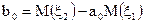 , уравнение регрессии - у =
, уравнение регрессии - у = 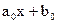 (Рис.16),
(Рис.16),
при этом дисперсия 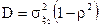 , и она является минимальной.
, и она является минимальной.
Таким образом, уравнение регрессии у = 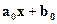 , дает наилучшее линейное представление ξ2 по ξ1.
, дает наилучшее линейное представление ξ2 по ξ1.
Количественной характеристикой нелинейной взаимосвязи случайных величин ξ1, ξ2 является корреляционное отношение. Коэффициент корреляционного отношения ξ2 по ξ1 вычисляется по формуле:
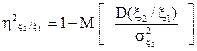 , (30)
, (30)
где 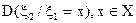 - условная дисперсия, характеризующая рассеяние ξ2 около условного математического ожидания
- условная дисперсия, характеризующая рассеяние ξ2 около условного математического ожидания 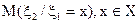 .
.
Свойства корреляционного отношения:
1. 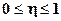 .
.
2. η=0 соответствует некоррелированным случайным величинам.
3. η=1,тогда и только тогда, когда имеет место функциональная зависимость между ξ1 и ξ2. В случае линейной зависимости ξ2 от ξ1 корреляционное отношение совпадает с квадратом коэффициента корреляции.
Корреляционное отношение несимметрично относительно ξ1 и ξ2, поэтому наряду с 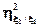 рассматривается
рассматривается 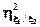 , определяемое аналогичным образом. Между
, определяемое аналогичным образом. Между 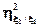 и
и 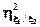 нет какой-либо простой зависимости.
нет какой-либо простой зависимости.
Теперь рассмотрим совокупность n-случайных величин 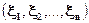 .Можно вычислить коэффициенты корреляции ρij между каждой парой случайных величин. Они составят корреляционную матрицу
.Можно вычислить коэффициенты корреляции ρij между каждой парой случайных величин. Они составят корреляционную матрицу
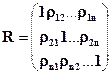
ρij=ρji, i≠j т.е. матрица симметрична относительно главной диагонали.
Взаимосвязь какой-либо случайной величины ξi со всеми остальными случайными величинами характеризуется множественным коэффициентом корреляции
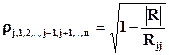 (31)
(31)
|R| - определитель матрицы R,
Rjj – алгебраическое дополнение, соответствующее элементу корреляционной матрицы ρjj,
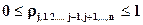 .
.
 2015-06-10
2015-06-10 792
792








