При практическом применении теории вероятностей часто приходиться встречаться с задачами, в которых в которых один и тот же опыт или аналогичные опыты повторяются неоднократно.
Определение 4.1. Последовательные испытания – это последовательное проведение 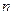 раз одного и того же опыта или одновременное проведение
раз одного и того же опыта или одновременное проведение 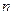 одинаковых опытов.
одинаковых опытов.
Определение 4.2. Говорят, что последовательные испытания удовлетворяют схеме Бернулли, если выполняются следующие условия:
- при каждом испытании различают лишь два исхода: событие А произошло или произошло его отрицание
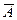 (то есть событие А не произошло);
(то есть событие А не произошло); - все испытания являются независимыми, то есть вероятность появления события А в k-ом испытании не зависит от исходов ни одного из испытаний до k-го;
- вероятность успеха в каждом испытании постоянна и равна
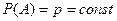 (вероятность неудачи при этом
(вероятность неудачи при этом 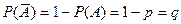 ).
).
Поставим своей задачей вычислить вероятность того, что при 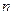 испытаниях событие А произошло ровно k раз и, следовательно, не произошло n-k раз. Искомую вероятность обозначают
испытаниях событие А произошло ровно k раз и, следовательно, не произошло n-k раз. Искомую вероятность обозначают 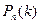 . Поставленную задачу решает так называемая формула Бернулли.
. Поставленную задачу решает так называемая формула Бернулли.
Теорема 4.1 (Формулы Бернулли). Пусть реализуется схема Бернулли. Тогда вероятность того, что в n испытаниях событие А наступит ровно k раз, равна
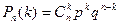 . . | (4.1) |
Вероятность того, что из n испытаний по схеме Бернулли событие А произойдет не менее l раз и не более m раз, равна
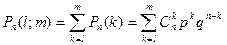 . . | (4.2) |
Вероятность того, что из n испытаний по схеме Бернулли событие А произойдет хотя бы один раз, равна
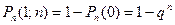 . . | (4.3) |
Пример 4.1. Оптовая база снабжает 5 магазинов, от каждого из которых может поступить заявка на очередной день с вероятностью 0,3 независимо от заявок других магазинов. Найти вероятность того, что в день 1) поступит три заявки; 2) не менее трех заявок; 3) хотя бы одна заявка.
Решение. Поступление или не поступление заявки можно рассматривать как одно испытание по схеме Бернулли, здесь 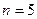 . Вероятность успеха (поступления заявки)
. Вероятность успеха (поступления заявки) 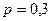 , вероятность неудачи
, вероятность неудачи 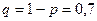 . Искомые вероятности вычислим, используя формулы Бернулли.
. Искомые вероятности вычислим, используя формулы Бернулли.
1. Используя формулу (4.1), получаем
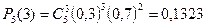 .
.
2. По формуле (4.2):
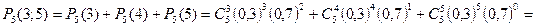
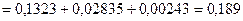 .
.
3. По формуле (4.3):
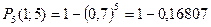 .
.
Определение 4.3. Число 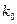 наступлений события А называется наивероятнейшим, если оно имеет наибольшую вероятность по сравнению с вероятностями наступления события А любое другое количество раз.
наступлений события А называется наивероятнейшим, если оно имеет наибольшую вероятность по сравнению с вероятностями наступления события А любое другое количество раз.
Теорема 4.2. Наивероятнейшее число наступлений события А в n испытаниях заключено между числами 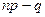 и
и 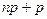 . При этом
. При этом
1. если число 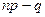 – дробное, то существует одно наивероятнейшее число
– дробное, то существует одно наивероятнейшее число 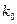 ;
;
2. если число 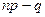 – целое, то существует два наивероятнейших числа, а именно:
– целое, то существует два наивероятнейших числа, а именно: 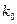 и
и 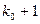 ;
;
3. если число 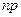 – целое, то наивероятнейшее число
– целое, то наивероятнейшее число 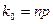 .
.
Пример 4.2. Испытывается каждый из 15 элементов некоторого устройства. Вероятность того, что элемент выдержит испытание, равна 0,9. Найти наивероятнейшее число элементов, которые выдержит испытание.
Решение. Из условия задачи: 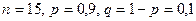 . Из теоремы 4.2. найдем наивероятнейшее число
. Из теоремы 4.2. найдем наивероятнейшее число 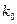 .
. 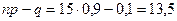 ,
, 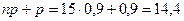 . Так как
. Так как 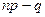 – дробное число, то существует одно наивероятнейшее число
– дробное число, то существует одно наивероятнейшее число 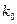 , заключенное между числами 13,5 и 14,4 и это число – 14. Таким образом,
, заключенное между числами 13,5 и 14,4 и это число – 14. Таким образом, 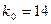 .
.
 2015-06-10
2015-06-10 2027
2027
