В случае, когда число испытаний 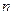 велико, формулу Бернулли применять неудобно. Для больших
велико, формулу Бернулли применять неудобно. Для больших 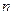 существуют приближенные формулы. Эти формулы тем точнее, чем
существуют приближенные формулы. Эти формулы тем точнее, чем 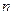 больше.
больше.
Рассмотрим сначала случай, когда с ростом 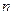 вероятность
вероятность 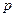 уменьшается обратно пропорционально
уменьшается обратно пропорционально 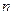 . При малых
. При малых 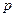 речь идет о появлении редких событий, так как вероятность их наступления в отдельном испытании мала. Однако вероятность появления одного или нескольких редких событий в длинной серии испытаний уже не будет малой величиной.
речь идет о появлении редких событий, так как вероятность их наступления в отдельном испытании мала. Однако вероятность появления одного или нескольких редких событий в длинной серии испытаний уже не будет малой величиной.
Теорема 4.3 (Формула Пуассона). Если вероятность 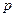 наступления события А в каждом испытании стремится к нулю
наступления события А в каждом испытании стремится к нулю 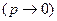 при неограниченном увеличении числа
при неограниченном увеличении числа 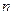 испытаний
испытаний 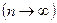 , причем произведение
, причем произведение 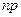 стремится к постоянному числу
стремится к постоянному числу 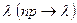 , то вероятность
, то вероятность 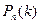 того, что событие А появится k раз в n независимых испытаниях, удовлетворяет предельному равенству
того, что событие А появится k раз в n независимых испытаниях, удовлетворяет предельному равенству
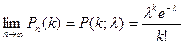 . . | (4.4) |
Из теоремы 4.3. следует, что если вероятность 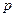 - постоянна и мала, число испытаний
- постоянна и мала, число испытаний 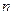 - велико и число
- велико и число 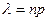 - незначительно (будем предполагать, что
- незначительно (будем предполагать, что 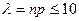 ), то из предельного равенства (4.4) вытекает приближенная формула Пуассона:
), то из предельного равенства (4.4) вытекает приближенная формула Пуассона:
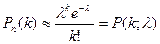 . . | (4.5) |
В таблице 1 приложений приведены значения функции Пуассона 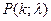 .
.
Пример 4.3. На факультете учиться 1825 студентов. Какова вероятность, что 1 сентября является днем рождением четырех студентов факультета?
Решение. Вероятность того, что день рождения студента 1 сентября, равна 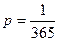 . Так как вероятность
. Так как вероятность 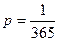 – мала, а число
– мала, а число 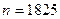 – велико и
– велико и 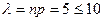 , то применяя формулу Пуассона (4.6):
, то применяя формулу Пуассона (4.6): 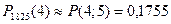 (по таблице 1 приложений).
(по таблице 1 приложений).
Теорема 4.4 (Локальная теорема Муавра-Лапласа). Если вероятность 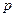 наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность
наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность 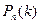 того, что событие А появится k раз в n независимых испытаниях при достаточно большом числе n, приближенно равна
того, что событие А появится k раз в n независимых испытаниях при достаточно большом числе n, приближенно равна
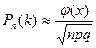 , , | (4.6) |
где
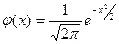 – – | (4.7) |
функция Гаусса, и
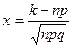 . . |
Чем больше n, тем точнее приближенная формула (4.6), называемая локальной формулой Муавра-Лапласа. Приближенные значения, даваемые локальной формулой (4.6), на практике используются при условии 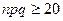 . Для функции Гаусса (4.7) составлена таблица ее значений (таблица 2, приведенная в приложении). Отметим, что функция Гаусса
. Для функции Гаусса (4.7) составлена таблица ее значений (таблица 2, приведенная в приложении). Отметим, что функция Гаусса 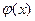 (4.7) обладает следующими очевидными свойствами.
(4.7) обладает следующими очевидными свойствами.
- Функция
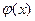 является четной, то есть
является четной, то есть 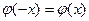 .
. - Функция
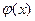 – монотонно убывающая при положительных значениях
– монотонно убывающая при положительных значениях 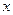 , причем при
, причем при 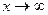
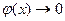 .
.
(Практически можно считать, что уже при 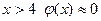 .)
.)
Пример 4.4. В некотором населенном пункте из каждых 100 семей 80 имеют холодильники. Найти вероятность того, что из 400 семей 300 имеют холодильники.
Решение. Вероятность того, что семья имеет холодильник, равна 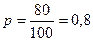 . Так как число
. Так как число 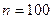 достаточно велико и условие
достаточно велико и условие 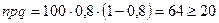 выполнено, то вычислим искомую вероятность, используя локальную формулу Муавра-Лапласа (4.6).
выполнено, то вычислим искомую вероятность, используя локальную формулу Муавра-Лапласа (4.6).
Из (4.7) определим 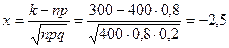 , тогда по формуле (4.6)
, тогда по формуле (4.6)
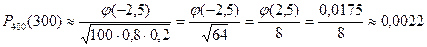
(значение 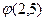 найдено по таблице 2 приложений ).
найдено по таблице 2 приложений ).
Теорема 4.5 (Интегральная теорема Муавра-Лапласа). Если вероятность 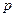 наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что число k наступления события А в n независимых испытаниях заключено в пределах от a до b (включительно), при достаточно большом числе n приближенно равна
наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что число k наступления события А в n независимых испытаниях заключено в пределах от a до b (включительно), при достаточно большом числе n приближенно равна
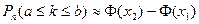 , , | (4.8) |
где
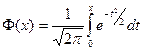 – – | (4.9) |
функция (или интеграл) Лапласа, и
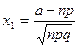 , , 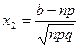 . . | (4.10) |
Чем больше n, тем точнее приближенная формула (4.8), называемая интегральной формулой Муавра-Лапласа. Так же, как и локальную формулу (4.6), на практике интегральная формула (4.8) используются при условии 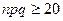 . Функции Лапласа (4.9) табулирована (таблица 3 приложения). Отметим следующие свойства функции.
. Функции Лапласа (4.9) табулирована (таблица 3 приложения). Отметим следующие свойства функции.
- Функция
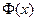 является нечетной, то есть
является нечетной, то есть 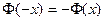 .
. - Функция
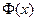 – монотонно возрастающая, причем при
– монотонно возрастающая, причем при 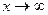
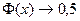 .
.
(Практически можно считать, что уже при 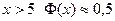 .)
.)
Пример 4.5. По данным примера 4.4 вычислить вероятность того, что от 300 до 360 семей (включительно) из 400 имеют холодильники.
Решение. Применим интегральную теорему Муавра-Лапласа ( 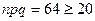 ). Вычислим значения
). Вычислим значения 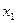 и
и 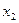 по формулам (4.10)
по формулам (4.10)
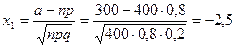 ,
, 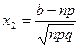
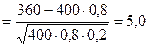 .
.
В силу формулы (4.8) и свойств функции 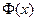 получаем
получаем
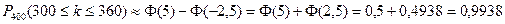 .
.
(по таблице 3 приложений 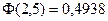 ,
, 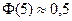 ).
).
 2015-06-10
2015-06-10 1837
1837








