Определение 3.4. Набор событий 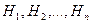 называется полной группой событий, если они попарно не пересекаются и их объединение есть достоверное событие:
называется полной группой событий, если они попарно не пересекаются и их объединение есть достоверное событие: 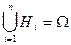 .
.
Теорема 3.4 (Формула полной вероятности). Пусть 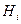 ,
, 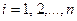 – полная группа событий, и
– полная группа событий, и 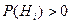 , тогда вероятность события А, которое может наступить лишь при выполнении одной из гипотез
, тогда вероятность события А, которое может наступить лишь при выполнении одной из гипотез 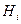 , равна
, равна
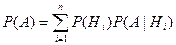 . . | (3.6) |
Теорема 3.5 (Формула Байеса). Пусть даны полная группа событий 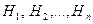 и некоторое событие А, которое может наступить лишь при появлении одной из гипотез
и некоторое событие А, которое может наступить лишь при появлении одной из гипотез 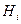 . Тогда для любого
. Тогда для любого 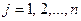 условная вероятность события
условная вероятность события 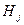 при условии, что событие А произошло, может быть вычислена по формуле
при условии, что событие А произошло, может быть вычислена по формуле
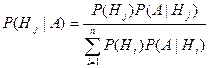 . . | (3.7) |
Пример 3.6. В урну, содержащую два шара, опущен белый шар, после чего из нее наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все возможные предположения о первоначальном составе шаров (по цвету).
Решение. Введем обозначения: событие A – извлечен белый шар. Возможны следующие гипотезы о первоначальном составе шаров:
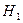 - нет белых шаров;
- нет белых шаров;
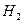 - один белый шар;
- один белый шар;
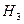 - два белых шара.
- два белых шара.
Данные гипотезы образуют полную группу, поэтому в силу теоремы 3.4 имеем:
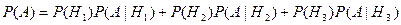 .
.
Так как по условию все гипотезы равновероятны и 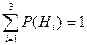 , то
, то
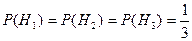 .
.
Вычислим теперь условные вероятности.
Условная вероятность того, что будет извлечен белый шар, при условии, что первоначально в урне не было белых шаров,
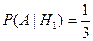 .
.
Условная вероятность того, что будет извлечен белый шар, при условии, что первоначально в урне был один белый шар,
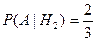 .
.
Условная вероятность того, что будет извлечен белый шар, при условии, что первоначально в урне было два белых шара,
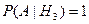 .
.
Окончательно получаем
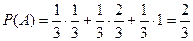 .
.
Пример 3.7. Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат дает 0,3% брака, второй – 1,5%. Наудачу берется деталь на проверку. Она оказалась бракованной. Какова вероятность, что она изготовлена первым автоматом?
Решение. Введем обозначения: событие A – деталь оказалась бракованной. Можно выдвинуть следующие гипотезы:
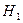 - деталь изготовлена первым автоматом;
- деталь изготовлена первым автоматом;
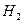 - деталь изготовлена вторым автоматом.
- деталь изготовлена вторым автоматом.
Так как первый автомат производит вдвое больше деталей, чем второй, то
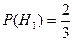 ,
, 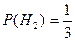 .
.
Условная вероятность того, что деталь будет бракованной, при условии, что она изготовлена первым автоматом,
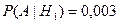 .
.
Условная вероятность того, что деталь будет бракованной, при условии, что она изготовлена вторым автоматом,
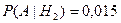 .
.
Тогда по формуле полной вероятности
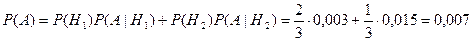 .
.
Искомая вероятность того, что бракованная деталь будет изготовлена первым автоматом, по формуле Байеса (3.7) равна
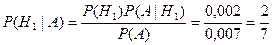 .
.
 2015-06-10
2015-06-10 1345
1345
