Рассмотрим положительную функцию
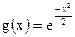
Докажите это, переходя к полярным координатам в интеграле 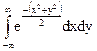 , который, очевидно, равен квадрату исходного. , который, очевидно, равен квадрату исходного.
| Так как
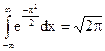 то функция
то функция
|
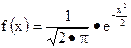
является плотностью и задает так называемое стандартное нормальное (гауссовское) распределение.
График этой плотности приведен на рисунке
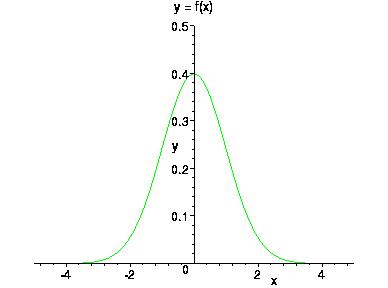
Общее нормальное распределение задается плотностью
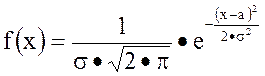
где
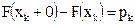
параметры распределения.
Покажите, что если 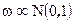 ,то ,то 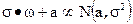
| Нормальное распределение обладает большим количеством замечательных свойств, многие из которых мы рассмотрим в дальнейшем. Это распределение использовал Гаусс Карл Фридрих в модели случайных ошибок измерения. Случайная величина, имеющая нормальное распределение, называется нормальная или гауссовская случайная величина. Для этого распределения используют обозначение |
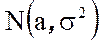 .
.
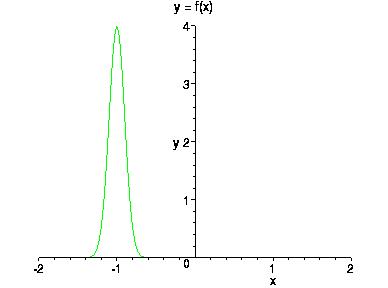
Графики плотности
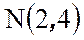
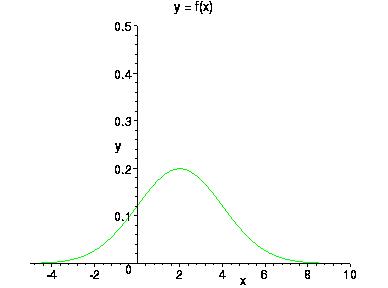
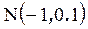
 2015-06-10
2015-06-10 348
348








