25. Лемма Маркова
Т. 1. Для любой положительной случайной величины Х вероятность того, что она примет значение, не превосходящее некоторого положительного числа 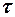 , больше разности между единицей и отношением математического ожидания этой случайной величины к данному числу
, больше разности между единицей и отношением математического ожидания этой случайной величины к данному числу 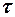 :
: 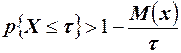 .
.
Доказательство. Проведём доказательство для дискретной случайной величины способом, получившим название метода урезания. Пусть 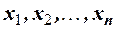 - упорядочная совокупность всех значений, принимаемых положительной случайной величиной Х с соответствующими вероятностями
- упорядочная совокупность всех значений, принимаемых положительной случайной величиной Х с соответствующими вероятностями 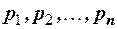 причём
причём 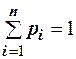 . Не нарушая общности доказательства, можно допустить, что значения случайной величины Х расположены в порядке убывания. Выберем некоторое произвольное число
. Не нарушая общности доказательства, можно допустить, что значения случайной величины Х расположены в порядке убывания. Выберем некоторое произвольное число 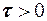 и предположим, что первые r значений совокупности больше
и предположим, что первые r значений совокупности больше 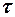 . Так как по условию случайная величина Х принимает только положительные значения, то можно записать неравенство
. Так как по условию случайная величина Х принимает только положительные значения, то можно записать неравенство
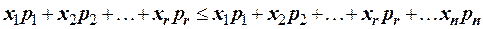 . По определению математического ожидания
. По определению математического ожидания 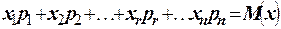 , следовательно
, следовательно 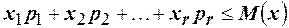 . Заменяя в левой части неравенства значения переменных
. Заменяя в левой части неравенства значения переменных 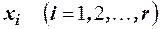 числом
числом 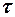 , получаем следующее усиленное неравенство
, получаем следующее усиленное неравенство 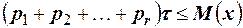 или
или 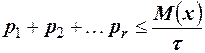 . Левая часть этого неравенства выражает вероятность того, что случайная величина принимает значения, большие
. Левая часть этого неравенства выражает вероятность того, что случайная величина принимает значения, большие 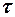 , то есть
, то есть 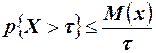 .
.
Вероятность противоположного события, а именно вероятность того, что случайная величина примет значения не больше 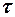 , определяется следующим неравенством:
, определяется следующим неравенством: 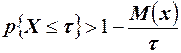 .
.
Лемма Маркова справедлива для любого распределения положительной случайной величины.
Пример 32. Среднее число студентов в группе, получивших на экзамене неудовлетворительные оценки, равно пяти. Оценить вероятность того, что в наудачу взятой группе будет более восьми двоек.
Решение. Используем неравенство Маркова. По условию задачи имеем 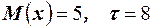 . Тогда искомая вероятность равна
. Тогда искомая вероятность равна 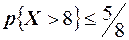 или
или 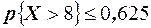 .
.
Т. Если случайная величина Х имеет конечные математическое ожидание и дисперсию, то для любого положительного числа 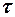 справедливо неравенство
справедливо неравенство 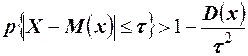 , то есть вероятность того, что отклонение случайной величины Х от своего математического ожидания по абсолютной величине не превзойдёт
, то есть вероятность того, что отклонение случайной величины Х от своего математического ожидания по абсолютной величине не превзойдёт 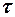 , больше разности между единицей и отношением дисперсии этой случайной величины к квадрату
, больше разности между единицей и отношением дисперсии этой случайной величины к квадрату 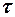 .
.
Доказательство. Воспользуемся леммой Маркова. Рассмотрим случайную величину 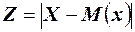 , для некоторых значений которой выполняется неравенство
, для некоторых значений которой выполняется неравенство 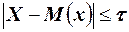 . Так как случайная величина Z положительна, то неравенства
. Так как случайная величина Z положительна, то неравенства 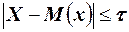 и
и 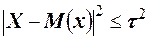 равносильны. Применив лемму Маркова к случайной величине
равносильны. Применив лемму Маркова к случайной величине 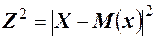 , получим
, получим
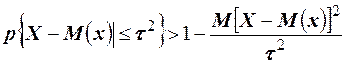 . Числитель дроби в правой части неравенства по определению есть дисперсия случайной величины Х, следовательно, неравенство можно записать в виде
. Числитель дроби в правой части неравенства по определению есть дисперсия случайной величины Х, следовательно, неравенство можно записать в виде 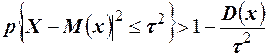 . Так как в силу равносильности соответствующих неравенств вероятности
. Так как в силу равносильности соответствующих неравенств вероятности 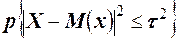 и
и 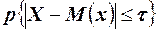 равны, то
равны, то 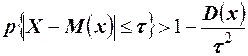 .
.
Неравенство Чебышева, как и неравенство Маркова, справедливо для любого распределения случайной величины Х, однако неравенство Чебышева применимо как к положительным, так и к отрицательным случайным величинам.
Полагая 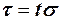 , запишем неравенство в виде
, запишем неравенство в виде
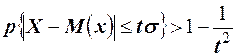 или
или 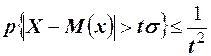 .
.
Задаваясь различными значениями t, вычислим верхние границы вероятностей того, что отклонение случайной величины выйдет за пределы 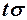 : при
: при 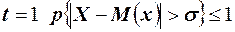 ;
;
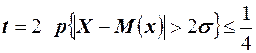 ;
; 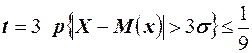 . Вероятности рассматриваемых событий не могут превысить этих числовых значений ни при каком распределении случайной величины.
. Вероятности рассматриваемых событий не могут превысить этих числовых значений ни при каком распределении случайной величины.
27. Теорема Чебышева
Т. При достаточно большом числе попарно независимых случайных величин 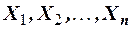 с математическими ожиданиями
с математическими ожиданиями 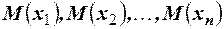 и дисперсиями
и дисперсиями 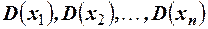 с вероятностью, близкой к единице, можно утверждать, что разность между средней арифметической наблюдавшихся значений случайных величин
с вероятностью, близкой к единице, можно утверждать, что разность между средней арифметической наблюдавшихся значений случайных величин 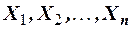 и средней арифметической их математических ожиданий по абсолютной величине окажется меньше сколь угодно малого числа
и средней арифметической их математических ожиданий по абсолютной величине окажется меньше сколь угодно малого числа 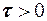 при условии, что дисперсия всех этих величин не превосходит одного и того же постоянного числа В, то есть
при условии, что дисперсия всех этих величин не превосходит одного и того же постоянного числа В, то есть
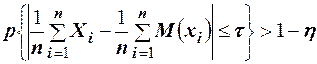 ,
,
где 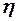 - положительное число, близкое к нулю.
- положительное число, близкое к нулю.
Доказательство. Пусть 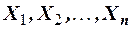 - п попарно независимых случайных величин. Средняя арифметическая этих величин является, в свою очередь, тоже случайной величиной. Обозначим её
- п попарно независимых случайных величин. Средняя арифметическая этих величин является, в свою очередь, тоже случайной величиной. Обозначим её 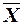 :
: 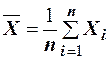 . Определим математическое ожидание и дисперсию
. Определим математическое ожидание и дисперсию 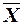 :
:
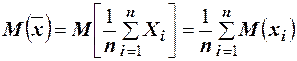 ,
,
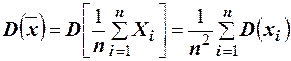 .
.
Применяя к случайной величине 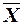 неравенство Чебышева, получаем
неравенство Чебышева, получаем
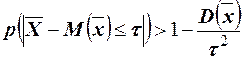 ,
,
или 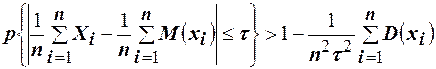 .
.
Заменяя в правой части последнего неравенства дисперсии случайных величин величиной В, которую по условию теоремы не превосходит ни одна из дисперсий, получаем усиленное неравенство
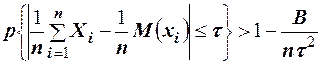 .
.
Для любого сколь угодно малого числа 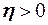 можно найти такое число п, при котором выполняется неравенство
можно найти такое число п, при котором выполняется неравенство 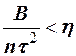 . Таким образом получаем неравенство, которое требовалось доказать:
. Таким образом получаем неравенство, которое требовалось доказать:
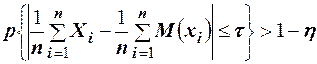 .
.
Переходя в фигурных скобках к противоположному событию, можно записать 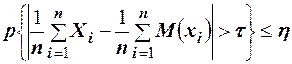 .
.
Теорема Чебышева показывает, средняя арифметическая попарно независимых случайных величин обладает свойством устойчивости и при определённых условиях мало отличается от средней арифметической математических ожиданий этих величин.
28. Основные понятия математической статистики
Математическая статистика - это раздел математики, изучающий методы сбора, систематизации и обработки результатов наблюдений массовых случайных явлений с целью выявления существующих закономерностей. Выводы о закономерностях, которым подчиняются явления, изучаемые методами математической статистики, всегда основываются на ограниченном, выборочном числе наблюдений. Поэтому естественно предположить, что эти выводы при большом числе наблюдений могут оказаться иными. Чтобы быть в состоянии высказать более определённое суждение об изучаемом явлении, математическая статистика опирается на теорию вероятностей.
Оценив неизвестные величины или зависимости между ними по данным наблюдений, исследователь выдвигает ряд гипотез, предположений о том, что рассматриваемое явление можно описать той или иной вероятностной теоретической моделью. Далее, используя математико-статистические методы, можно дать ответ на вопрос, какую из гипотез или моделей следует принять. Именно эта модель и есть закономерность изучаемого явления.
Основные задачи математической статистики состоят в разработке методов:
1) организации и планирования статистических наблюдений;
2) сбора статистических данных;
3) «свертка информации», то есть методов группировки и сокращения статистических данных с целью сведения большого числа таких данных к небольшому числу параметров, которые в сжатом виде характеризуют всю исследуемую совокупность;
4) анализа статистических данных;
5) принятия решений, рекомендаций и выводов на основе анализа статистических данных;
6) прогнозирования случайных явлений.
Одним из основных методов статистического наблюдения является выборочный метод. Рассмотрим основные понятия этого метода.
29. Вариационные ряды
О. 1. Генеральной совокупностью называется совокупность всех мыслимых наблюдений, которые могли бы быть сделаны при данном реальном комплексе условий измерений. Число членов, образующих генеральную совокупность, называется объёмом генеральной совокупности.
О. 2. Выборочной совокупностью или просто выборкой объёмом п называется совокупность п объектов, отобранных из исследуемой генеральной совокупности.
О. 3. Вариантами называются различные значения признака, а варьированием – изменение значений признака.
О. 4. Расположение наблюдаемых значений в порядке возрастания или убывания называется ранжированием выборки.
О. 5. Если признак по своей сущности таков, что различные значения не могут отличаться друг от друга меньше чем на некоторую конечную величину, то говорят, что это дискретно варьирующийся признак.
О. 6. Число, показывающее, сколько раз встречается вариант х в ряде наблюдений, называется частотой варианта mx.
Вместо частоты варианта х можно рассматривать её отношение к общему числу наблюдений п, которое называется частостью варианта х и обозначается 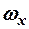 . Так как общее число наблюдений равно сумме частот всех вариантов
. Так как общее число наблюдений равно сумме частот всех вариантов 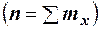 , то справедлива следующая цепочка равенств:
, то справедлива следующая цепочка равенств: 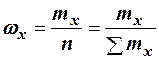 .
.
О. 7. Таблица, позволяющая судить о распределении частот (или частостей) между вариантами, называется дискретным вариационным рядом.
Наряду с понятием частоты используется понятие накопленной частоты, которую обозначают 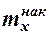 . Накопленная частота показывает, во скольких наблюдениях признак принял значения, меньшие заданного значения х. Отношение накопленной частоты к общему числу наблюдений называют накопленной частостью и обозначают
. Накопленная частота показывает, во скольких наблюдениях признак принял значения, меньшие заданного значения х. Отношение накопленной частоты к общему числу наблюдений называют накопленной частостью и обозначают 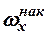 . Очевидно, что
. Очевидно, что 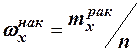 .
.
О. 8. Признак называется непрерывно варьирующим, если он может принять любое значение в некотором числовом интервале.
По полученным данным такого признака трудно выявить характерные черты варьирования значений признака. Построение дискретного вариационного ряда также не даст желаемых результатов (слишком велико число вариантов). Для получения ясной картины нужно объединить полученные значения в несколько интервалов.
О. 9. Таблицу, позволяющую судить о распределении частот (или частостей) между интервалами варьирования значений признака, называют интервальным вариационным рядом.
Интервальный вариационный ряд строят по данным наблюдений за непрерывно варьирующим признаком, а также за дискретно варьирующим, если велико число наблюдавшихся вариантов. Дискретный вариационный ряд строят только для дискретно варьирующего признака.
Для построения интервального вариационного ряда необходимо определить величину интервала, установить полную шкалу интервалов, в соответствии с ней сгруппировать результаты наблюдений. Для определения оптимального интервала h, то есть такого, при котором построенный интервальный ряд не был бы слишком громоздким и в то же время позволял выявить характерные черты рассматриваемого явления, можно использовать формулу Стэрджеса 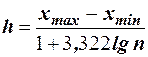 , где
, где 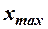 и
и 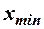 - соответственно максимальный и минимальный варианты. Величина
- соответственно максимальный и минимальный варианты. Величина 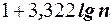 характеризует число интервалов m, но так как количество интервалов целое число, то её округляют до целого значения. При этом желательно, чтобы
характеризует число интервалов m, но так как количество интервалов целое число, то её округляют до целого значения. При этом желательно, чтобы 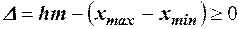 было минимальным для возможных значений m. Длина интервала имеет ту же точность, что и варианты.
было минимальным для возможных значений m. Длина интервала имеет ту же точность, что и варианты.
Пример 33. Найти оптимальную длину интервала по следующим данным, 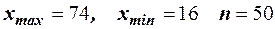 , причём значения вариантов целые числа.
, причём значения вариантов целые числа.
Решение. Вычислим 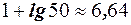 . Возможные количество интервалов 7 или 6. Соответствующие им длины интервалов равны
. Возможные количество интервалов 7 или 6. Соответствующие им длины интервалов равны 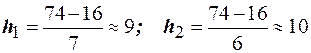 . Тогда
. Тогда 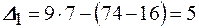 и
и 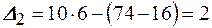 . Так как
. Так как 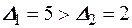 , то для уменьшения погрешностей желательно взять шесть интервалов, имеющих длину 10.
, то для уменьшения погрешностей желательно взять шесть интервалов, имеющих длину 10.
30. Графическое изображение вариационного ряда.
Графическое изображение вариационного ряда позволяет представить в наглядной форме закономерности варьирования значений признака. Наиболее широко используются следующие виды графического изображения вариационных рядов: полигон, гистограмма, кумулятивная кривая.
Полигон, как правило, служит для изображения дискретного вариационного ряда. Для его построения в прямоугольной системе координат наносят точки с координатами 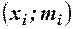 , где
, где 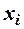 -вариант,
-вариант, 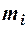 -соответствующая ему частота. Иногда вместо точек
-соответствующая ему частота. Иногда вместо точек 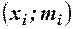 строят точки
строят точки 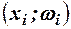 . Затем эти точки последовательно соединяют отрезками в порядке возрастания
. Затем эти точки последовательно соединяют отрезками в порядке возрастания 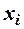 . Полученная линия носит название полигон частот или полигон относительных частот. Иногда интервальный ряд изображают с помощью полигона. В этом случае интервалы заменяют их серединными значениями и к ним относят интервальные частоты. Для полученного дискретного ряда строят полигон.
. Полученная линия носит название полигон частот или полигон относительных частот. Иногда интервальный ряд изображают с помощью полигона. В этом случае интервалы заменяют их серединными значениями и к ним относят интервальные частоты. Для полученного дискретного ряда строят полигон.
Гистограмма служит для изображения только интервального вариационного ряда. Для её построения в прямоугольной системе координат по оси абсцисс откладывают отрезки, изображающие интервалы варьирования, и на них строят прямоугольники с высотами, равными частотам (или частостям) соответствующего интервала. В результате получают ступенчатую фигуру, состоящую из прямоугольников, которую называют гистограммой.
Кумулятивная кривая (кривая накопленных частот или накопленных частостей) строится следующим образом. Если вариационный ряд дискретный, то в прямоугольной системе координат строят точки с координатами 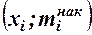 , где xi - вариант,
, где xi - вариант, 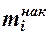 - соответствующая накопленная частота. Иногда вместо точек
- соответствующая накопленная частота. Иногда вместо точек 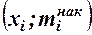 строят точки
строят точки 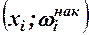 . Полученные точки соединяют отрезками.
. Полученные точки соединяют отрезками.
Если вариационный ряд интервальный, то по оси абсцисс откладывают интервалы. Верхним границам интервалов соответствуют накопленные частоты (или накопленные частости); нижней границе первого интервала – накопленная частота, равная нулю. Построив кумулятивную кривую, можно приблизительно установить число наблюдений (или их долю в общем количестве наблюдений), в которых признак принял значения, меньшие заданного. Иногда кумулятивную кривую называют кумулятой.
Пример 34. Построить полигон частот, гистограмму, кумуляту для интервального вариационного ряда.
| Интервалы | 4 - 8 | 8 - 12 | 12 -16 | 16 - 20 | 20 –24 | 24 -28 |
| Частоты |
Решение. Построим полигон частот. Вынесем на координатную плоскость точки 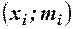 , где
, где 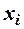 - середины соответствующих интервалов, то есть точки
- середины соответствующих интервалов, то есть точки 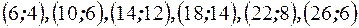 . Соединив их ломаной кривой, получим полигон частот.
. Соединив их ломаной кривой, получим полигон частот.

Для построения гистограммы отложим на оси абсцисс интервалы варьирования и на них как на основаниях построим прямоугольники высотами, равными соответствующим частотам.
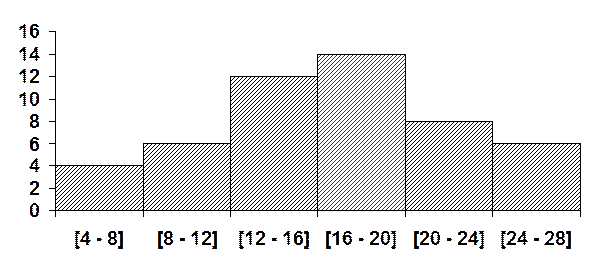
Для построения кумулятивной кривой отложим на координатной плоскости точки (4;0), (8;4), (12;10), (16;22), (20;36), (24;44), (28;45) и соединим их ломаной линией, получим кумуляту.

31. Эмпирическая функция распределения
Эмпирической функцией распределения случайной величины Х называют функцию 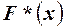 , определяющую для каждого значения х частость события
, определяющую для каждого значения х частость события 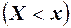 :
: 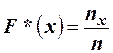 , где пх – число вариантов хi, меньших х; п – объём выборки.
, где пх – число вариантов хi, меньших х; п – объём выборки.
Эмпирическая функция распределения обладает всеми свойствами интегральной функции распределения. Действительно, из определения эмпирической функции распределения следует, что:
1) значения эмпирической функции распределения принадлежат отрезку 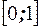 ;
;
2) 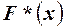 - неубывающая функция;
- неубывающая функция;
3) если х1 - наименьшее, а хп – наибольшее наблюденное значение, то 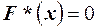 при
при 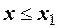 и
и 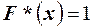 при
при 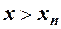 .
.
Основное значение эмпирической функции распределения состоит в том, что она используется в качестве оценки функции распределения 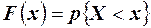 .
.
Пример 35. Построить эмпирическую функцию распределения для вариационного ряда
| Варианты | ||||
| Частота |
Решение. Согласно определению эмпирическая функция распределения имеет вид
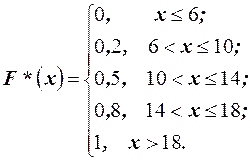
И её график имеет вид
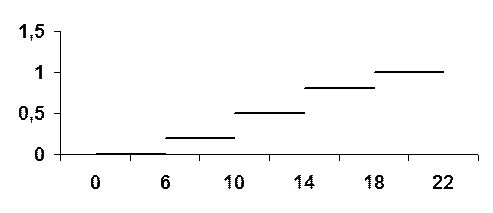
32. Средние величины
Средние величины являются как бы «представителями» всего ряда наблюдений, поскольку вокруг них концентрируются наблюдавшиеся значения признака. Заметим, что только для качественно однородных наблюдений имеет смысл вычислять средние величины.
Различают несколько видов средних величин: средняя арифметическая, средняя геометрическая, средняя гармоническая, средняя квадратическая, средняя кубическая и так далее. При выборе вида средней величины необходимо ответить на вопрос: какое свойство ряда мы хотим представить средней величиной или, иначе говоря, какая цель преследуется при вычислении средней? Это свойство, получившее название определяющего, и определяет вид средней. Понятие определяющего свойства впервые введено советским статистиком А. Я. Боярским.
Наиболее распространенной средней величиной является средняя арифметическая. Пусть 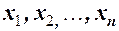 - данные наблюдений;
- данные наблюдений; 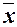 - средняя арифметическая. Свойство, определяющее среднюю арифметическую, формулируется следующим образом: сумма результатов наблюдений должна остаться неизменной, если каждое из них заменить средней арифметической, то есть
- средняя арифметическая. Свойство, определяющее среднюю арифметическую, формулируется следующим образом: сумма результатов наблюдений должна остаться неизменной, если каждое из них заменить средней арифметической, то есть 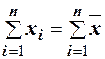 . Так как
. Так как 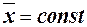 , то
, то 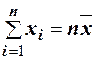 . Отсюда получаем следующую формулу для вычисления средней арифметической по данным наблюдений:
. Отсюда получаем следующую формулу для вычисления средней арифметической по данным наблюдений: 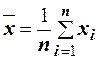 . Если по наблюдениям построен вариационный ряд, то средняя арифметическая
. Если по наблюдениям построен вариационный ряд, то средняя арифметическая 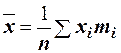 , где
, где 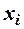 - вариант, если ряд дискретный, и середина интервала, если ряд интервальный;
- вариант, если ряд дискретный, и середина интервала, если ряд интервальный; 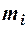 - соответствующая частота.
- соответствующая частота.
Очевидно, что если по данным наблюдений построен дискретный вариационный ряд, то обе формулы дают одинаковые значения средней арифметической. Если же по наблюдениям построен интервальный ряд, то средние арифметические, вычисленные по этим формулам могут не совпадать, так как во второй формуле значения признака внутри каждого интервала принимаются равными центрам интервалов. Ошибка, возникающая в результате такой замены, вообще говоря, очень мала, если наблюдения распределены равномерно вдоль каждого интервала, а не скапливаются к одноимённым границам интервалов.
Основные свойства средней арифметической.
1. Сумма отклонений результатов наблюдений от средней арифметической равна нулю, или сумма произведений отклонений вариантов от средней арифметической на соответствующие частоты равна нулю.
2. Если все результаты наблюдений уменьшить (увеличить) на одно и то же число, то средняя арифметическая уменьшится (увеличится) на это же число.
3. Если все результаты наблюдений уменьшить (увеличить) в одно и то же число раз, то средняя арифметическая уменьшится (увеличится) во столько же раз.
4. Средняя арифметическая алгебраической суммы соответствующих значений признака нескольких рядов наблюдений с одинаковым числом наблюдений равна алгебраической сумме средних арифметических этих рядов.
О.1. Среднюю арифметическую вычисленную по данным выборки называют выборочной средней.
Пример 36. Найти выборочную среднюю для выборки, представленной интервальным вариационным рядом
| Интервалы | 3 - 7 | 7 - 11 | 11 - 15 | 15 - 19 | 19 - 23 | 23 – 27 |
| Частоты |
Решение. Середины интервалов равны: 5; 9; 13; 17; 21; 25. Сумма частот равна 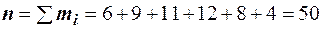 . Тогда выборочная средняя равна
. Тогда выборочная средняя равна
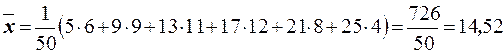 .
.
 2015-06-10
2015-06-10 2479
2479
