14. Закон распределения случайной величины
О. 1. Случайной называют величину, которая принимает в результате испытания то или иное (но при этом только одно) возможное значение, заранее неизвестное, меняющееся от испытания к испытанию и зависящее от случайных обстоятельств.
В отличие от случайного события, являющегося качественной характеристикой случайного результата испытания, случайная величина характеризует результат испытания количественно.
О. 2. Дискретной называют такую случайнуювеличину, которая принимает конечное или бесконечное счётное множество значений.
Примером дискретной случайной величины могут являться: число дефектных деталей в партии, число заявок, число отказов элементов за определённое время и так далее.
О. 3. Непрерывной называют такую случайную величину, которая может принимать любые значения из некоторого конечного или бесконечного интервала. Примером непрерывной случайной величины могут являться время безотказной работы отдельных элементов системы, погрешность измерения физических величин.
Случайные величины обычно обозначаются заглавными буквами конца латинского алфавита – X, Y, Z,…., а их возможные значения – соответствующими малыми буквами – x, y, z,…
Для задания случайной величины недостаточно перечислить все её возможные значения. Необходимо также знать, как часто могут появляться те или иные значения в результате испытаний при одних и тех же условиях, то есть нужно задать вероятности их появления.
О. 4. Законом распределения случайной величины называется всякое соотношение между возможными значениями случайной величины и соответствующими вероятностями.
О. 5. Две случайные величины называются независимыми, если распределение вероятности одной из них не зависит от того, какие возможные значения приняла другая величина. В противном случае случайные величины называются зависимыми.
О. 6. Таблица, содержащая возможные значения случайной величины и соответствующие вероятности, называется рядом распределения случайной величины.
Пример 18. Составить закон распределения числа появлений герба при трёх бросаниях монеты.
Решение. Случайная величина X - число появлений герба может принимать значения: 0; 1; 2; 3. Соответствующие вероятности найдём по формуле Бернулли, используя то, что вероятность появления герба в одном испытании равна 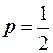 .
.
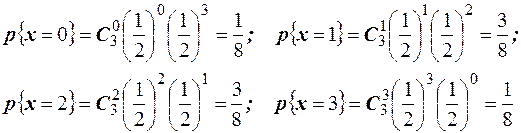
Следовательно, ряд распределения имеет вид:
| xi | ||||
| pi | 1/8 | 3/8 | 3/8 | 1/8 |
Функция распределения является наиболее общей формой задания закона распределения случайной величины. Она используется как для дискретных, так и для непрерывных случайных величин. Обычно обозначается F(x).
О. 1. Функция распределения определяет вероятность того, что случайная величина Х примет значение, меньше фиксированного действительного числа х, то есть 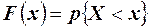 .
.
Вероятность того, что 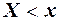 , зависит от х, следовательно, F(x) является функцией от х. Поэтому F(x) называется функцией распределения. В литературе встречаются термины: «интегральная функция распределения» и «интегральный закон распределения».
, зависит от х, следовательно, F(x) является функцией от х. Поэтому F(x) называется функцией распределения. В литературе встречаются термины: «интегральная функция распределения» и «интегральный закон распределения».
Общие свойства функции распределения.
1. Функция распределения F(x) есть неотрицательная функция, заключённая между нулём и единицей: 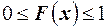 .
.
2. Функция распределения случайной величины есть неубывающая функция, то есть из 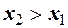 следует
следует 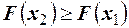 .
.
3. На минус бесконечности функция распределения равна нулю, а на плюс бесконечности функция распределения равна единице, то есть 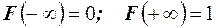 .
.
Следует отметить, что в то время, как каждая случайная величина однозначно определяет функцию распределения, одну и ту же функцию распределения могут иметь различные случайные величины. Отсюда следует второе определение случайной величины.
О. 2. Случайной величиной называется переменная величина, значения которой зависят от случая и для которой определена функция распределения вероятностей.
Т. 1. Вероятность попадания случайной величины в интервал 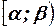 равна разности значений на концах интервала:
равна разности значений на концах интервала:
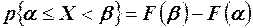 .
.
Доказательство. Рассмотрим три события: А, состоящее в том, что 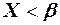 ; событие В, состоящее в том, что
; событие В, состоящее в том, что 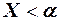 ; событие С, состоящее в том, что
; событие С, состоящее в том, что 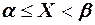 . Тогда
. Тогда 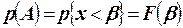 ;
; 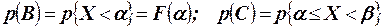 .
.
Очевидно, что событие А представляет собой сумму двух несовместных событий В и С. По теореме сложения вероятностей 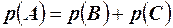 , или
, или 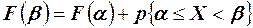 , откуда
, откуда 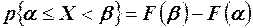 .
.
Следствие. Вероятность любого отдельного значения непрерывной случайной, величины равна нулю.
Пример 19. Составить функцию распределения для ряда распределения из примера 18.
Решение. Сумма вероятностей при 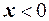 равна нулю, следовательно, для любого
равна нулю, следовательно, для любого 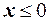 имеем
имеем 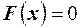 , при
, при 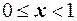 сумма вероятностей равна
сумма вероятностей равна 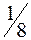 , поэтому для любого
, поэтому для любого 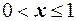 имеем
имеем 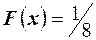 , при
, при 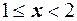 сумма вероятностей равна
сумма вероятностей равна 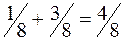 , поэтому для любого
, поэтому для любого 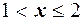 имеем
имеем 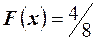 , при
, при 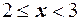 сумма вероятностей равна
сумма вероятностей равна 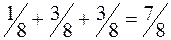 , поэтому для любого
, поэтому для любого 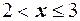 имеем
имеем 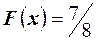 , при
, при 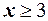 сумма вероятностей равна
сумма вероятностей равна 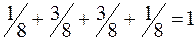 , поэтому для любого
, поэтому для любого 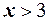 имеем
имеем 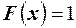 . Тогда функция распределения имеет вид
. Тогда функция распределения имеет вид
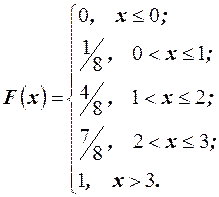
Полученная функция имеет ступенчатый вид.
Непрерывную случайную величину можно задать не только интегральной функцией распределения, но и дифференциальной функцией. Рассмотрим эту форму задания распределения случайной величины. Пусть задана непрерывная случайная величина Х с функцией распределения 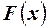 . Тогда, если существует
. Тогда, если существует 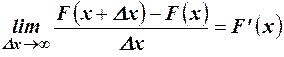 , то функция
, то функция 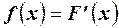 называется дифференциальной функцией распределения или плотностью распределения.
называется дифференциальной функцией распределения или плотностью распределения.
Используя методы интегрального исчисления, можно предложить формулу для нахождения интегральной функции распределения по плотности 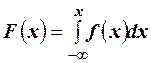 .
.
Свойства плотности распределения.
1. Плотность распределения больше либо равна нулю для любого значения аргумента, то есть 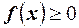 . Так как интегральная функция распределения неубывающая, следовательно, её производная неотрицательная.
. Так как интегральная функция распределения неубывающая, следовательно, её производная неотрицательная.
2. Вероятность попадания случайной величины в заданный интервал 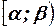 находится по формуле
находится по формуле 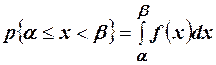 .
.
3. Условие нормировки. Интеграл в бесконечных пределах от плотности распределения равен единице, 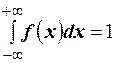 .
.
Пример 20. Случайная величина Х подчинена закону распределения с плотностью 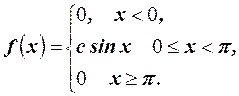 .
.
Определить коэффициент с. Найти вероятность попадания случайной величины на участок от 0 до 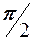 и функцию распределения.
и функцию распределения.
Решение. Площадь, ограниченная кривой распределения, равна 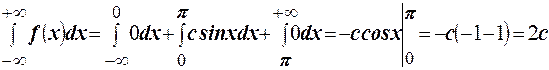 , по условию нормировки получаем
, по условию нормировки получаем 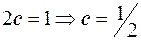 . Вероятность попадания в интервал найдём по формуле
. Вероятность попадания в интервал найдём по формуле
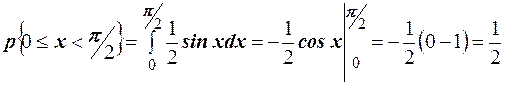 .
.
Интегральную функцию распределения найдём по формуле 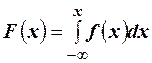 . Для
. Для 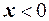 : имеем
: имеем 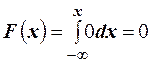 .
.
Для 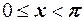 :
:
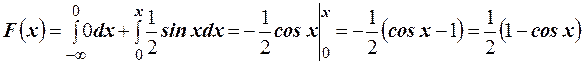 .
.
Для 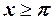 :
: 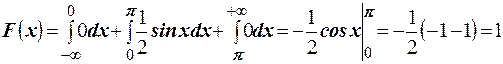 .
.
Следовательно, интегральная функция распределения имеет вид
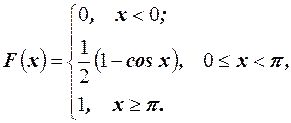
Математическое ожидание определяет положение случайной величины на числовой оси, показывая центр распределения (некоторое среднее значение, около которого сосредоточены все возможные значения случайной величины).
О. 1. Математическим ожиданием дискретной случайной величины называют сумму произведений всех возможных значений на их вероятности, то есть 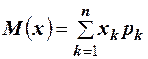 .
.
О. 2. Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат интервалу 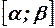 , находится по формуле
, находится по формуле 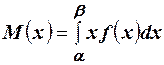 .
.
Основные свойства математического ожидания.
1. Математическое ожидание постоянной равно самой постоянной, 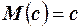 .
.
2. Постоянный множитель выносится за знак математического ожидания, 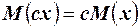 .
.
3. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий, 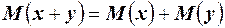 .
.
4. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, 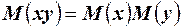 .
.
5. Математическое ожидание отклонения случайной величины от её математического ожидания равно нулю, 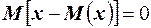 .
.
Пример 21. Найти математическое ожидание для случайной величины, заданной функцией распределения:
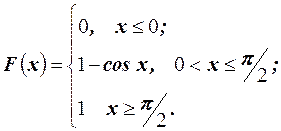
Решение. Найдём плотность распределения из соотношения
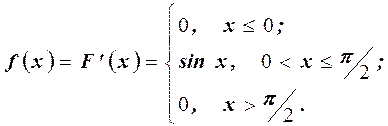
Математическое ожидание непрерывной случайной величины находим по формуле
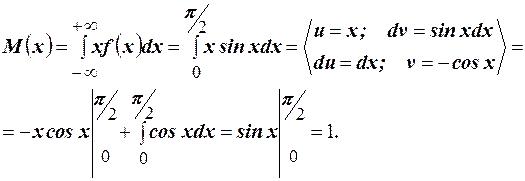 Пример 22. Найти математическое ожидание для ряда
Пример 22. Найти математическое ожидание для ряда
| xi | ||||
| pi | 0,1 | 0,3 | 0,4 | 0,5 |
распределения
Решение. Для дискретной случайной величины используем формулу 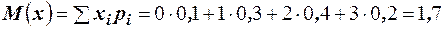 .
.
О. 3. Модой М0 дискретной случайной величины называется её значение, имеющее наибольшую вероятность.
О. 4. Модой М0 непрерывной случайной величины называется такое её значение, при котором плотность распределения имеет максимум.
Геометрически моду можно интерпретировать как абсциссу точки максимума кривой распределения. Бывают двухмодальные и многомодальные распределения. Встречаются распределения, которые имеют минимум, но не имеют максимума. Такие распределения называются антимодальными.
О. 5. Медианой случайной величины Ме называют такое её значение, для которого справедливо равенство 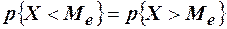 , то есть равновероятно, что случайная величина окажется больше или меньше медианы.
, то есть равновероятно, что случайная величина окажется больше или меньше медианы.
С геометрической точки зрения, медиана – абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам. Так как вся площадь, ограниченная кривой распределения и осью абсцисс, равна единице, то функция распределения в точке, соответствующей медиане, равна 0,5:
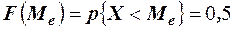 .
.
18. Дисперсия и среднее квадратическое отклонение
О. 1. Дисперсией случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания 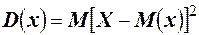 .
.
Дисперсия характеризует меру рассеяния случайной величины вокруг математического ожидания. Недостатком дисперсии является то, что она имеет размерность квадрата случайной величины и её неудобно использовать для характеристики разброса.
Этих недостатков лишено среднее квадратическое отклонение случайной величины, которое представляет собой квадратный корень из дисперсии 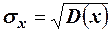 .
.
Основные свойства дисперсии.
1. Дисперсия постоянной величины равна нулю, 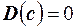 .
.
Доказательство. 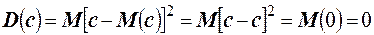 .
.
2. Постоянный множитель случайной величины можно выносить за знак дисперсии, предварительно возведя его в квадрат 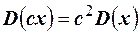 .
.
Доказательство. По свойствам математического ожидания
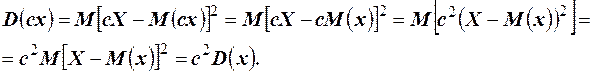
3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин 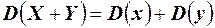 .
.
Доказательство. Используя определение дисперсии и свойство математического ожидания 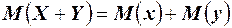 , дисперсию случайной величины
, дисперсию случайной величины 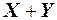 можно выразить следующим образом:
можно выразить следующим образом: 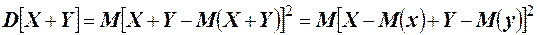 .
.
Представим выражение в квадратных скобках в виде двучлена и запишем квадрат его суммы. Используя свойства математического ожидания суммы и произведения двух независимых случайных величин, получаем
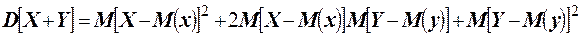 .
.
Согласно свойству 5 математического ожидания, второе слагаемое равно нулю, следовательно: 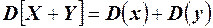 .
.
4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий, 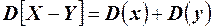 .
.
Доказательство. На основании свойства 3 можно записать 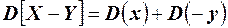 . Согласно свойству 2 имеем
. Согласно свойству 2 имеем 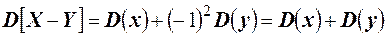 .
.
5. Дисперсия случайной величины Х, равна разности между математическим ожиданием квадрата случайной величины Х и квадратом её математического ожидания, 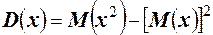 .
.
Доказательство. Используя определение дисперсии и свойства математического ожидания, имеем
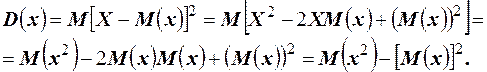
Пример 23. Найти дисперсию для распределения непрерывной случайной величины, заданной в примере 21.
Решение. В примере 21 было найдено математическое ожидание 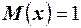 . Для нахождения дисперсии используем её 5 свойство. Вычислим
. Для нахождения дисперсии используем её 5 свойство. Вычислим
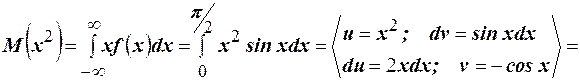
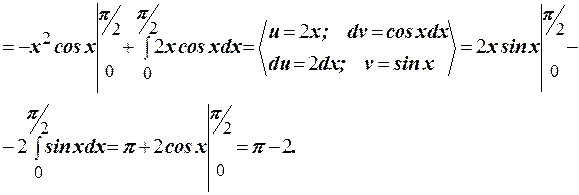
Тогда дисперсия равна 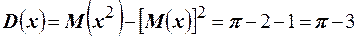 .
.
| xi | ||||
| pi | 0,1 | 0,3 | 0,4 | 0,2 |
Пример 24. Найти дисперсию и среднее квадратическое отклонение для дискретной случайной величины, имеющей ряд распределения
Решение. Математическое ожидание для этого распределения найдено в примере 22, и оно равно 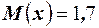 . Для нахождения дисперсии вычислим
. Для нахождения дисперсии вычислим
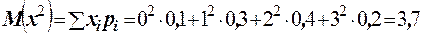 . Тогда дисперсия равна
. Тогда дисперсия равна 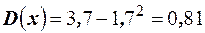 . Среднее квадратическое отклонение найдём по формуле
. Среднее квадратическое отклонение найдём по формуле 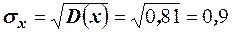 .
.
Пример 25. Дискретная случайная величина Х имеет только два возможных значения: х 1 и х 2, причём х 1< х 2. Вероятность того, что Х примет значение х 1, равна 0,5. Найти закон распределения Х, зная математическое ожидание 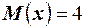 и
и 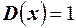 .
.
Решение. Используя условие нормировки 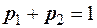 , найдём
, найдём 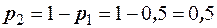 . Так как
. Так как 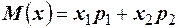 , то
, то 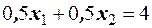 или
или 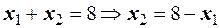 . По пятому свойству дисперсии
. По пятому свойству дисперсии 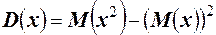 , где
, где
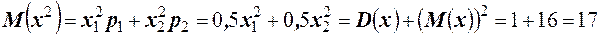 или
или 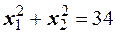 . Подставив в полученное уравнение
. Подставив в полученное уравнение 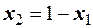 , получим
, получим 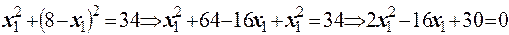 или
или 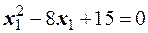 . Решая полученное квадратное уравнение, находим
. Решая полученное квадратное уравнение, находим 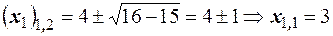 и
и 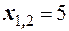 , тогда
, тогда 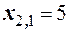 и
и 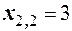 . По условию задачи х 1< х 2, следовательно: х 1=3
. По условию задачи х 1< х 2, следовательно: х 1=3
| xi | ||
| pi | 0,5 | 0,5 |
и х 2=5, и искомый закон распределения имеет вид
19. Начальные и центральные моменты
О. 1. Начальным моментом k -го порядка случайной величины называют математическое ожидание величины Xk, 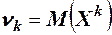 .
.
Начальный момент для дискретной случайной величины 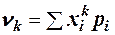 .
.
Начальный момент для непрерывной случайной величины 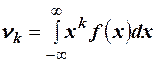 .
.
О. 2. Центральным моментом k -го порядка случайной величины называют математическое ожидание величины 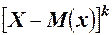 ,
, 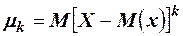 .
.
Центральный момент для дискретной случайной величины 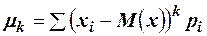 .
.
Центральный момент для непрерывной случайной величины 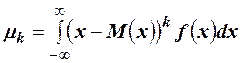 .
.
Соотношения между начальными и центральными моментами 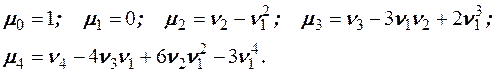
Начальный момент первого порядка представляет собой математическое ожидание 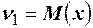 , а центральный момент второго порядка дисперсию случайной величины
, а центральный момент второго порядка дисперсию случайной величины 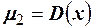 .
.
О. 3. Нормированный центральный момент третьего порядка служит характеристикой скошенности или асимметрии распределения (коэффициент асимметрии) 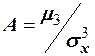 .
.
О. 4. Нормированный центральный момент четвёртого порядка служит характеристикой островершинности или плосковершинности распределения (эксцесс), 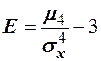 .
.
Пример 26. Случайная величина Х задана плотностью распределения 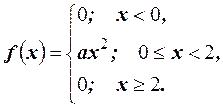
Найти коэффициент а, математическое ожидание, дисперсию, коэффициенты асимметрии и эксцесса.
Решение. Площадь, ограниченная плотностью распределения, численно равна 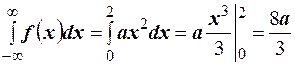 . Учитывая, что эта площадь должна быть равна единице, находим
. Учитывая, что эта площадь должна быть равна единице, находим 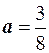 .
.
Найдём начальные моменты.
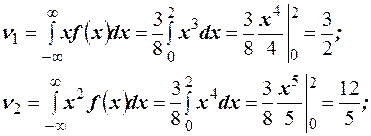
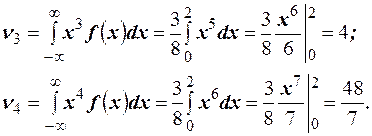
Найдём центральные моменты.
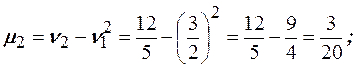
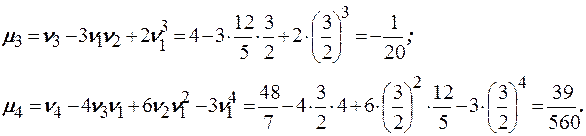
Тогда математическое ожидание равно 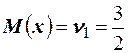 , дисперсия равна
, дисперсия равна 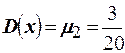 . Асимметрия
. Асимметрия 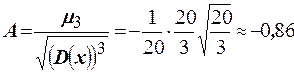 и эксцесс
и эксцесс 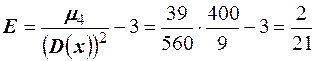 .
.
О. 1. Непрерывная случайная величина Х имеет равномерное распределение на интервале 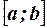 , если на этом интервале плотность распределения постоянна, а вне его равна нулю,
, если на этом интервале плотность распределения постоянна, а вне его равна нулю,
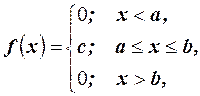 где с -const.
где с -const.
Найдём значение постоянной с. Так как площадь, ограниченная кривой распределения, равна единице и все значения случайной величины принадлежат интервалу 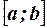 , то должно выполняться равенство
, то должно выполняться равенство 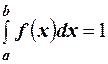 , или
, или 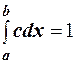 , отсюда
, отсюда
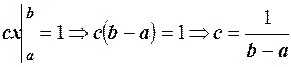 .
.
Следовательно, плотность распределения можно записать в виде
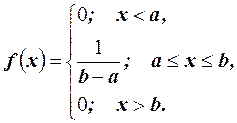
Интегральная функция распределения имеет вид
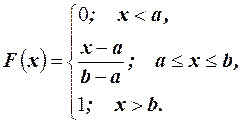
Определим основные числовые характеристики случайной величины, имеющей равномерное распределение. Математическое ожидание 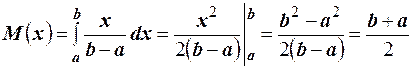 .
.
В силу симметричности распределения медиана совпадает с математическим ожиданием 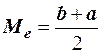 . Моды равномерное распределение не имеет. Дисперсия равномерного распределения равна
. Моды равномерное распределение не имеет. Дисперсия равномерного распределения равна 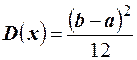 . В силу симметричности коэффициент асимметрии равен нулю. Коэффициент эксцесса равен
. В силу симметричности коэффициент асимметрии равен нулю. Коэффициент эксцесса равен 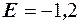 .
.
Пример 27. Цена деления амперметра равна 0,1 А. Показания округляются до ближайшего целого деления. Найти вероятность того, что при отсчёте будет сделана ошибка, превышающая 0,02А. Вычислить математическое ожидание и дисперсию.
Решение. Ошибку округления можно рассматривать как случайную величину Х, которая распределена равномерно в интервале между двумя соседними целыми делениями. Плотность равномерного распределения 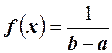 , где
, где 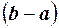 - длина интервала, в котором заключены возможные значения, вне интервала
- длина интервала, в котором заключены возможные значения, вне интервала 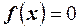 . В рассматриваемом примере длина интервала, в котором заключены возможные значения Х, равна 0,1, поэтому
. В рассматриваемом примере длина интервала, в котором заключены возможные значения Х, равна 0,1, поэтому 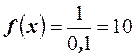 . Ошибка отсчёта превысит 0,02, если она будет заключена в интервале
. Ошибка отсчёта превысит 0,02, если она будет заключена в интервале 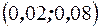 . По формуле
. По формуле 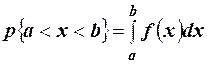 получим
получим
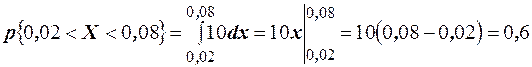 . Математическое ожидание равно
. Математическое ожидание равно 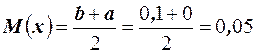 . Дисперсия равна
. Дисперсия равна 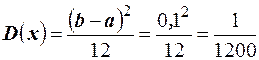 .
.
 2015-06-10
2015-06-10 4066
4066
