Р(A+B)=Р(A)+Р(B),
где А, В - несовместные события.
Следствие 1. 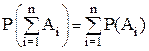 , где Аi, i=1,..., n – попарно-несовместные события.
, где Аi, i=1,..., n – попарно-несовместные события.
Следствие 2. Если A1 ,A2 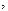 ..., An полная группа событий, то
..., An полная группа событий, то
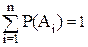 .
.
Следствие 3. Если А и 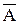 противоположные события, то
противоположные события, то
Р(А)+Р(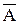 )=1
)=1
Следствие (из теорем сложения и умножения). Вероятность появления хотя бы одного из событий 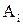 , i =1,..., n, независимых в совокупности
, i =1,..., n, независимых в совокупности
Р(А)=1 – 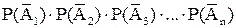 .
.
Если Р(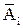 ) =q, то Р(А)=1 – qn.
) =q, то Р(А)=1 – qn.
Пример. В читальном зале имеется 6 учебников по теории вероятностей, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найти вероятность того, что оба учебника окажутся в переплете.
Решение. Рассмотрим следующие события:
А1– первый взятый учебник в переплете;
A2– второй взятый учебник в переплете.
Событие, состоящее в том, что оба взятых учебника в переплете 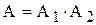 . События А1 и А2 являются зависимыми, так как вероятность наступления события А2 зависит от наступления события А1. Для решения указанной задачи воспользуемся теоремой умножения вероятностей зависимых событий:
. События А1 и А2 являются зависимыми, так как вероятность наступления события А2 зависит от наступления события А1. Для решения указанной задачи воспользуемся теоремой умножения вероятностей зависимых событий:
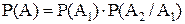 .
.
Вероятность наступления события А1 p(A1) в соответствии с классическим определением вероятности:
P(A1) = 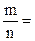
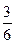 = 0,5.
= 0,5.
Вероятность наступления события А2 определяется условной вероятностью наступления события А2 при условии наступления события А1, т.е.
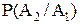 =
= 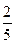 =0,4.
=0,4.
Тогда искомая вероятность наступления события:
P(A)=0,5  0,4=0,2.
0,4=0,2.
Пример. Два стрелка делают по одному выстрелу в мишень. Вероятность попадания первого стрелка – 0,9; второго стрелка – 0,8. Найти вероятность того, что:
а) в мишень попадет только один стрелок;
б) мишень будет поражена.
Решение:
а) Пусть событие А - в мишень попадет только один стрелок. Введем события: 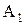 - в мишень попадет первый стрелок;
- в мишень попадет первый стрелок; 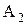 - в мишень попадет второй стрелок. Согласно условию:
- в мишень попадет второй стрелок. Согласно условию: 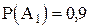 ;
; 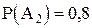 .
.
Заметим, что событие А означает следующее: в мишень попадет только первый стрелок (то есть первый попадет и второй не попадет) или в мишень попадет только второй стрелок (то есть второй попадет и первый не попадет). Тогда 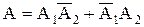 . События
. События 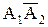 и
и 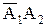 несовместны, так как имеют множители, являющиеся противоположными событиями. Значит, к ним применима теорема сложения вероятностей для несовместных событий. События
несовместны, так как имеют множители, являющиеся противоположными событиями. Значит, к ним применима теорема сложения вероятностей для несовместных событий. События 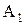 и
и 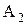 независимы, значит, наступление
независимы, значит, наступление 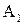 не изменяет вероятности
не изменяет вероятности 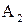 . Из этого следует, что и ненаступление
. Из этого следует, что и ненаступление 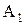 (то есть наступление
(то есть наступление 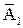 ) не меняет вероятности
) не меняет вероятности 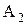 . Значит, независимы
. Значит, независимы 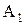 и
и 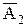 ,
, 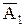 и
и 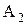 , и к этим парам событий применима теорема умножения независимых событий. Учитывая, что
, и к этим парам событий применима теорема умножения независимых событий. Учитывая, что 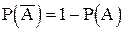 , имеем:
, имеем:
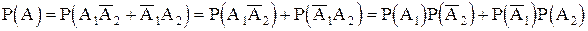 =
=
=0,9(1-0,8)+(1-0,9)0,8=0,9  0,2+0,1
0,2+0,1  0,8=0,18+0,08=0,26.
0,8=0,18+0,08=0,26.
б) Пусть событие В - мишень будет поражена. Это произойдет, если в мишень попадет хотя бы один стрелок: или только первый, или только второй, или оба (и первый, и второй). Значит 
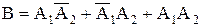
 . Рассуждая аналогично пункту а), имеем:
. Рассуждая аналогично пункту а), имеем:
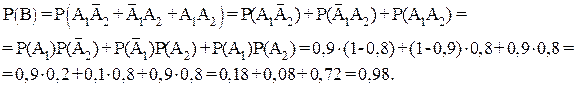
Найти вероятность события В можно, используя теорему сложения совместных событий 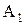 и
и 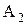 . Согласно определению суммы событий
. Согласно определению суммы событий 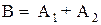 .
.
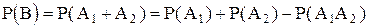 =
=
= 0,9+0,8-0,9  0,8 = 1,7- 0,72 = 0,98.
0,8 = 1,7- 0,72 = 0,98.
Найти вероятность события В можно, используя подход “от противного”. Событием, противоположным к В, является событие 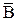 - ни один стрелок не попадет в мишень. Тогда имеем:
- ни один стрелок не попадет в мишень. Тогда имеем:
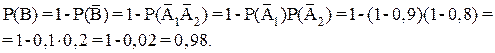
 2015-06-10
2015-06-10 1093
1093
