Геометрическая вероятность используется в случае, когда число равновозможных исходов бесконечно. Геометрической вероятностью, характеризующей вероятность появления случайной точки внутри некоторой области, называется отношение размера этой области к размеру всей области, в которой может появляться данная точка
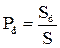 , где
, где
Рd - вероятность попадания случайной точки в область Sd;
S - общая область, где может появляться случайная точка.
Пример. Выпущено 100 лотерейных билетов, причем установлены призы, из которых 8 по 1 руб., 2- по 5 руб. и 1-10 руб. Найти вероятность того, что купленный билет выиграл: а) 5 рублей; б) не более 5 рублей.
Решение: а) Для определения искомой вероятности используем формулу классического определения вероятности Р(A)= 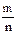 . Определим общее число исходов n. Оно равно числу выпущенных билетов-100. Определим благоприятное число исходов m. Оно равно числу лотерейных билетов с выигрышем в 5 рублей, т.е. 2. Тогда искомая вероятность равна: Р(А)=
. Определим общее число исходов n. Оно равно числу выпущенных билетов-100. Определим благоприятное число исходов m. Оно равно числу лотерейных билетов с выигрышем в 5 рублей, т.е. 2. Тогда искомая вероятность равна: Р(А)= 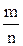 =
= 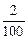 =0,02.
=0,02.
б) Условие выигрыш “не более 5 рублей” означает, что купленный билет должен иметь либо выигрыш, равный 1 рублю (таких билетов 8), либо выигрыш, равный 5 рублям (таких билетов 2).В данном случае общее число исходов, как и в пункте а) равно 100, а число благоприятных исходов равно 10=8+2. Тогда искомая вероятность равна: Р(А)= 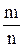 =
= 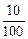 =0,1.
=0,1.
Пример. В цехе работают шесть мужчин и четыре женщины. По табельным номерам наудачу отобраны семь человек. Найти вероятность того, что среди отобранных лиц окажутся три женщины.
Решение. Для решения указанной задачи воспользуемся классическим определением вероятности Р(A)= 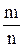 , где А - событие, состоящее в том, что отобраны по табельным номерам три женщины и четверо мужчин; m- число исходов, благоприятствующих появлению событию А; n- общее число исходов. Общее число возможных исходов испытания равно числу способов, которыми можно отобрать семь человек из десяти. Число способов определяется по выражению:
, где А - событие, состоящее в том, что отобраны по табельным номерам три женщины и четверо мужчин; m- число исходов, благоприятствующих появлению событию А; n- общее число исходов. Общее число возможных исходов испытания равно числу способов, которыми можно отобрать семь человек из десяти. Число способов определяется по выражению: 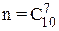 .
.
Число исходов, благоприятствующих появлению события А, определяется числом способов, которым можно отобрать трех женщин из четырех, т.е. 
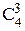 и четырех мужчин из шести, т.е.
и четырех мужчин из шести, т.е. 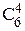 . Следовательно, число исходов, благоприятствующих появлению события А: m=
. Следовательно, число исходов, благоприятствующих появлению события А: m= 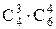 .
.
Искомая вероятность:
Р(A)= 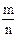 =
= 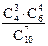 =
= 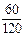 =0,5.
=0,5.
Пример. В квадрат со сторонами равными а наудачу бросается точка. Определить вероятность того, что точка попадет внутрь вписанного в квадрат круга. Данная задача решается с использованием формулы геометрического определения вероятности. Мерой пространства элементарных событий 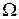 является площадь квадрата
является площадь квадрата 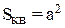 .
.
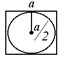 |
Площадь круга - мера события А. 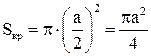 .
.
Тогда искомая вероятность будет определяться по формуле. 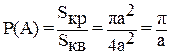
ЗАДАЧИ
1.Лотерея состоит из 1000 билетов, среди них 150 выигрышных. Наугад вынимается 1 билет из 1000. Чему равна вероятность того, что этот билет выигрышный?
2. При броске игральной кости вычислить вероятности следующих событий:
а) выпало 2 очка;
б) выпало 5 очков;
в) выпало простое число очков;
г) число выпавших очков кратно трем;
д) выпало нечетное число очков.
3. В замке на общей оси пять дисков. Каждый диск разделен на шесть секторов, на которых написаны различные буквы. Замок открывается только в том случае, если каждый диск занимает одно определенное положение относительно корпуса замка. Найти вероятность того, что при произвольной установке дисков замок можно будет открывать.
4. В мешочке имеется пять одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: О,П,Р,С,Т. Найти вероятность того, что на вынутых по одному и расположенных в одну линию кубиков можно прочесть слово “ спорт”.
5.В лотерее 100 билетов, из них 40 выигрышных. Какова вероятность того, что когда сначала юноша, а потом девушка вытянут по одному билету, то окажется:
а) что юноша взял выигрышный билет, а девушка – нет;
б) что у девушки оказался выигрышный билет;
в) что у обоих билеты не выигрышные.
6. Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстоянии 2а. На плоскость наудачу брошена монета радиуса r < а. Найти вероятность того, что монета не пересеет ни одной прямой.
7. На отрезок АВ длины L наудачу брошена точка С с координатой х. Найти вероятность того, что меньший из отрезков АС и ВС имеет длину большую, чем 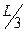 .
.
8. На отрезок ОА длины L числовой оси ОХ наудачу брошены две точки В(х) и С(у). Найти вероятность того, что длина отрезка ВС меньше расстояния от точки О до ближайшей к ней точки.
9. На отрезок ОА длины L числовой оси ОХ наудачу брошены две точки В(х) и С(у), причем 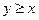 . Найти вероятность того, что длина отрезка ВС меньше длины отрезка ОВ.
. Найти вероятность того, что длина отрезка ВС меньше длины отрезка ОВ.
10. На отрезок ОА длины L числовой оси ОХ наудачу брошены две точки В(х) и С(у). Найти вероятность того, что длина отрезка ВС окажется меньше, чем 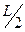 .
.
 2015-06-10
2015-06-10 5748
5748
