Т1. Пусть имеется 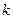 , (
, (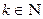 ) групп элементов, причем
) групп элементов, причем 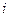 -я группа содержит
-я группа содержит 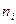 элементов,
элементов, 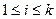 . Выберем из каждой группы по одному элементу. Тогда общее число
. Выберем из каждой группы по одному элементу. Тогда общее число 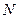 способов, которыми можно произвести такой выбор, равняется
способов, которыми можно произвести такой выбор, равняется
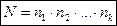
Представим результат выбора, описанного в теореме 1, в виде набора 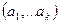 , в котором
, в котором 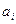 — выбранный из
— выбранный из 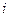 -й группы элемент. Тогда общее число различных наборов
-й группы элемент. Тогда общее число различных наборов 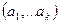 также равняется
также равняется 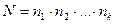 .
.
► Занумеруем элементы 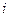 -й группы числами от 1 до
-й группы числами от 1 до 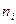 . Элемент из первой группы можно выбрать
. Элемент из первой группы можно выбрать 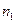 способами. Если мы выбрали элемент
способами. Если мы выбрали элемент 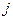 ,
, 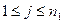 , то выбрать элемент из второй группы мы можем
, то выбрать элемент из второй группы мы можем 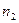 способами. Получаем, что с первым элементом
способами. Получаем, что с первым элементом 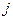 возможно составить
возможно составить 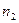 пар
пар 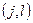 , где
, где 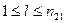 .
.
Но столько же пар можно составить и с любым другим элементом первой группы. Тогда всего пар, в которых первый элемент выбран из первой группы, а второй — из второй, существует ровно 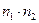 .
.
Иначе говоря, есть 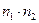 способов выбрать по одному элементу из первых двух групп. Возьмем одну такую пару
способов выбрать по одному элементу из первых двух групп. Возьмем одну такую пару 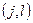 . Заметим, что элемент из третьей группы можно выбрать
. Заметим, что элемент из третьей группы можно выбрать 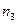 способами, то есть возможно составить ровно
способами, то есть возможно составить ровно 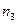 троек
троек 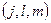 , добавляя к данной паре
, добавляя к данной паре 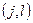 любой из
любой из 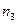 элементов третьей группы.
элементов третьей группы.
Но столько же троек можно составить и с любой другой парой 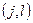 . Тогда всего троек, в которых первый элемент выбран из первой группы, второй — из второй, а третий — из третьей, существует ровно
. Тогда всего троек, в которых первый элемент выбран из первой группы, второй — из второй, а третий — из третьей, существует ровно 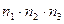 .
.
Продолжая рассуждения, методом математической индукции заключаем справедливость утверждения теоремы. ◄
 2015-06-10
2015-06-10 748
748








