Т. Общее количество выборок в схеме выбора 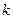 элементов из
элементов из  с возвращением и с учетом порядка определяется формулой
с возвращением и с учетом порядка определяется формулой
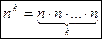 . (6)
. (6)
¨ Первый шарик можно выбрать  способами. При каждом из этих способов второй шарик можно выбрать также
способами. При каждом из этих способов второй шарик можно выбрать также  способами, и так
способами, и так 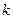 раз. ¨
раз. ¨
Таким образом, размещениями с повторениями называются комбинации из  элементов по
элементов по 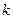 элементов, отличающиеся составом и порядком их расположения.
элементов, отличающиеся составом и порядком их расположения.
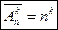 . (7)
. (7)
Пример 5. Сколько двузначных чисел можно составить из цифр 1- 4? §Так как повторения цифр в числе возможны, то производим выборку с возвращением. Двузначные числа представляют собой комбинации из 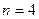 элементов по
элементов по 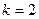 элементов. Следовательно, согласно формуле (7) искомое количество чисел определяется числом размещений
элементов. Следовательно, согласно формуле (7) искомое количество чисел определяется числом размещений
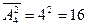 .
.
Это числа: 11, 12, 13, 14, 21, 22, 23, 24, 31, 32, 33, 34, 41, 42, 43, 44. §
Опр. Размещением данного состава 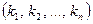 из элементов
из элементов  - членного множества
- членного множества 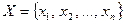 называется всякая строка длинной
называется всякая строка длинной 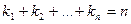 , составленная из элементов множества
, составленная из элементов множества  , так, что элемент
, так, что элемент 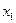 повторяется
повторяется 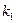 раз, элемент
раз, элемент 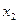 –
– 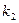 раз и т.д., элемент
раз и т.д., элемент 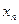 –
– 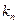 раз.
раз.
Например, если 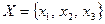 , то
, то 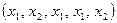 есть размещение состава (3,2,0).
есть размещение состава (3,2,0).
Количество различных размещений заданного состава 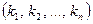 называется числом перестановок с повторениями и равно:
называется числом перестановок с повторениями и равно:
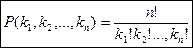 . (8)
. (8)
Пример 6. Сколькими способами можно поставить на книжной полке 3 экземпляра учебника по алгебре, 2 экземпляра учебника по геометрии и один экземпляр учебника по математическому анализу?
§ Очевидно, всякой расстановке указанных учебников взаимно однозначно соответствует строка длиной 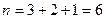 состава
состава 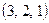 . Следовательно, искомое число способов равно числу размещений с повторениями:
. Следовательно, искомое число способов равно числу размещений с повторениями: 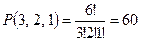 . §
. §
 2015-06-10
2015-06-10 667
667








