Т. Общее количество выборок в схеме выбора 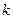 элементов из
элементов из  с возвращением и без учета порядка определяется формулой
с возвращением и без учета порядка определяется формулой
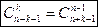
и называется числом сочетаний с повторениями.
Без доказательства.
При решении задач комбинаторики используются следующие правила:
Правило суммы:
Если объект 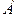 может быть выбран
может быть выбран  способами,
способами,  -
- 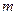 способами, то или
способами, то или  , или
, или  может быть выбран
может быть выбран 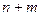 способами.
способами.
Правило произведения:
Если объект 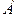 может быть выбран
может быть выбран  способами, и после каждого такого выбора объект
способами, и после каждого такого выбора объект  – может быть выбран
– может быть выбран 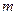 способами, то пара
способами, то пара 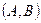 в указанном порядке (!) может быть выбрана
в указанном порядке (!) может быть выбрана 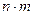 способами. То же справедливо и для нескольких выбираемых объектов.
способами. То же справедливо и для нескольких выбираемых объектов.
Пример 7. Сколькими способами можно составить четырехзначное число, все цифры которого различны?
§ Каждому четырехзначному числу можно поставить во взаимно однозначное соответствие строку 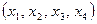 , где
, где 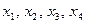 – соответственно 1, 2, 3 и 4-я цифры. Элемент
– соответственно 1, 2, 3 и 4-я цифры. Элемент 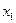 этой строки можно выбрать 9 способами (любую из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9); элемент
этой строки можно выбрать 9 способами (любую из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9); элемент 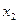 можно выбрать также 9 способами (теперь можно использовать и цифру 0, но первую выбранную цифру повторить нельзя); элемент
можно выбрать также 9 способами (теперь можно использовать и цифру 0, но первую выбранную цифру повторить нельзя); элемент 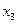 можно выбрать 8 способами (уже выбранные первые две цифры повторить нельзя); наконец, элемент
можно выбрать 8 способами (уже выбранные первые две цифры повторить нельзя); наконец, элемент 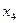 можно выбрать 7 способами. Выборка производится с учетом порядка. Согласно правилу произведения искомое число способов выбора четырехзначного числа с различными цифрами равно: 9 × 9 × 8 × 7 = 4536. §
можно выбрать 7 способами. Выборка производится с учетом порядка. Согласно правилу произведения искомое число способов выбора четырехзначного числа с различными цифрами равно: 9 × 9 × 8 × 7 = 4536. §
Пример 8. Из 10-и гвоздик и 6-и тюльпанов составляются букеты, каждый из которых должен содержать 3 гвоздики и 2 тюльпана. Сколько можно составить различных букетов?
§ Производится выборка без возвращения и без учета порядка. Из шестнадцати элементов (цветов) необходимо выбрать пять, причем три из них должны быть гвоздиками, а два – тюльпанами. Три гвоздики мы выбираем 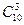 способами, а два тюльпана -
способами, а два тюльпана - 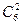 способами. Следовательно, искомое количество различных букетов равно
способами. Следовательно, искомое количество различных букетов равно
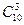 ∙
∙ 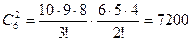 . §
. §
 2015-06-10
2015-06-10 1046
1046
