Опр. Непрерывной называют случайную величину, которая может принимать все значения из некоторого промежутка (конечного или бесконечного). ·
Число возможных значений непрерывной случайной величины бесконечно.
Для НСВ неприменим способ задания ДСВ (перечень всех возможных значений и их вероятности). Рассмотрим СВ  , возможные значения которой сплошь заполняют интервал
, возможные значения которой сплошь заполняют интервал 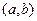 . Составить перечень всех возможных ее значений невозможно. Необходимо дать общий способ задания любых типов СВ. С этой целью вводят функции распределения вероятностей СВ.
. Составить перечень всех возможных ее значений невозможно. Необходимо дать общий способ задания любых типов СВ. С этой целью вводят функции распределения вероятностей СВ.
Пусть  - действительное число. Вероятность события, состоящего в том, что
- действительное число. Вероятность события, состоящего в том, что  примет значение, меньшее чем
примет значение, меньшее чем  , т.е. вероятность события
, т.е. вероятность события 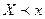 , обозначим через
, обозначим через 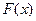 . С изменением
. С изменением  меняется и
меняется и 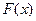 .
.
Опр. Функцией распределения называют функцию 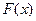 , определяющую вероятность того, что СВ
, определяющую вероятность того, что СВ  в результате испытания примет значение, меньшее чем
в результате испытания примет значение, меньшее чем  , т.е.
, т.е.
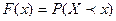 . · (1)
. · (1)
Иногда вместо термина «функция распределения» используют термин «интегральная функция».
Функция распределения (ФР) является общей характеристикой, описывающей как ДСВ, так и НСВ.
Геометрическая интерпретация ФР: ФР есть вероятность того, что СВ примет значение, которое изображается на числовой оси точкой, лежащей левее точки  .
.
Для ДСВ  , которая может принимать значения
, которая может принимать значения 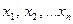 , ФР будет иметь вид:
, ФР будет иметь вид:
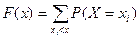 , (2)
, (2)
где символ 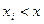 обозначает, что суммирование распространяется на все те возможные значения СВ, которые по своей величине меньше аргумента
обозначает, что суммирование распространяется на все те возможные значения СВ, которые по своей величине меньше аргумента  .
.
Из (2) следует, что ФР ДСВ  разрывна и возрастает скачками при переходе через точки возможных ее значений
разрывна и возрастает скачками при переходе через точки возможных ее значений 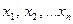 , причем величина скачка равна вероятности соответствующего значения.
, причем величина скачка равна вероятности соответствующего значения.
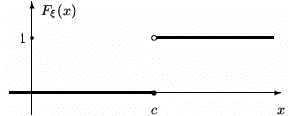
Пример. Случайная величина  имеет вырожденное распределение
имеет вырожденное распределение 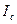 .
.
Тогда 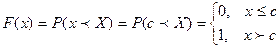 .
.
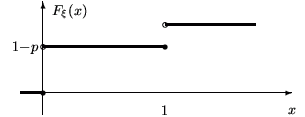
Пример. Случайная величина  имеет распределение Бернулли
имеет распределение Бернулли 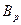 . Тогда
. Тогда 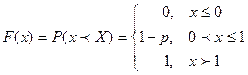 .
.
Пример 1. ДСВ задана таблицей распределения. Найти функцию распределения и начертить ее график.
 | |||
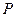 | 0,3 | 0,1 | 0,6 |
1. Если 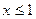 , то
, то 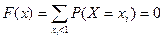 .
.
2. Если 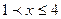 , то
, то 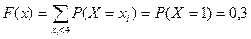 .
.
3. Если 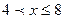 , то
, то 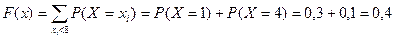 . Действительно, если
. Действительно, если 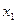 удовлетворяет неравенству
удовлетворяет неравенству 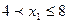 , то
, то 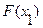 равно вероятности события
равно вероятности события 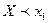 , которое может быть осуществлено, когда
, которое может быть осуществлено, когда  примет значение 1 с вероятностью 0,3 или значение 4 с вероятностью 0,1. Поскольку эти два события несовместны, то по теореме сложения вероятность события
примет значение 1 с вероятностью 0,3 или значение 4 с вероятностью 0,1. Поскольку эти два события несовместны, то по теореме сложения вероятность события 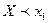 равна сумме вероятностей 0,3+0,1=0,4.
равна сумме вероятностей 0,3+0,1=0,4.
4. Если 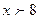 , то
, то 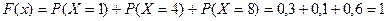
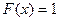 . Действительно, событие
. Действительно, событие 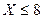 достоверно, Þ его вероятность равна единице.
достоверно, Þ его вероятность равна единице.
 Итак, функция распределения аналитически может быть записана так:
Итак, функция распределения аналитически может быть записана так:




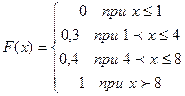 . График:
. График:
0 1 4 8
 2015-06-10
2015-06-10 877
877








