Свойства функция распределения

Свойство 1. Значения функции распределения принадлежат отрезку :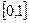

.

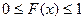► Это вытекает из определения вероятности.◄

Свойство 2. Вероятность того, что СВ примет значение, заключенное в интервале 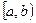, равна приращению функции распределения на этом интервале:

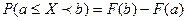. (3)

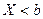► Рассмотрим события: – СВ 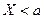; 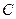– СВ ; – СВ .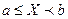

Очевидно, событие представляет собой сумму двух несовместных событий и 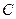, т.е.

.

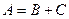По теореме сложения вероятностей несовместных событий имеем:

.

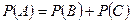Но

;

;

.

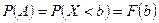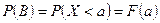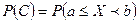Поэтому

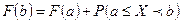(4)

Отсюда следует (3). ◄

Следствие. Вероятность того, что НСВ примет одно определенное значение, равна нулю.

► Перейдем в равенстве (4) к пределу при :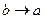

(*)

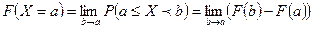Значение этого предела зависит от того, является ли непрерывной функция 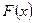в точке 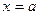или же терпит разрыв. Если в точке 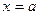функция 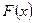имеет разрыв, то предел (*) равен значению скачка функции 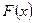в точке 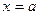. Если же функция 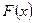в точке 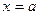непрерывна, то этот предел равен нулю.

Так как НСВ имеет непрерывную ФР 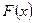, то из равенства нулю предела для непрерывной функции 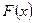в точке 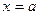следует, что и вероятность любого отдельного значения НСВ равна нулю. ◄

Свойство 3. 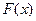- неубывающая функция, т.е. 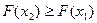, если .

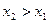► Это свойство вытекает из свойства 2. Действительно, согласно выражению (4) имеем: 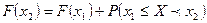. Но, так как вероятность любого события не может быть отрицательной, то 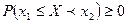. А это значит, что 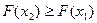, если . ◄

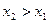Свойство 4. Если возможные значения СВ принадлежат интервалу 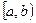, то:

.

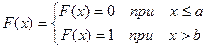Следствие. Если возможные значения СВ расположены на всей оси , то справедливы следующие предельные соотношения:

.

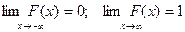График функции распределения.

График функции распределения СВ – кривая распределения - расположен в полосе, ограниченной прямыми 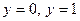. При возрастании в интервале 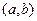, график «подымается вверх». При 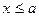ординаты графика равны нулю; при 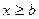- равны единице.

Свойство 5. Случайная величина имеет дискретное распределение тогда и только тогда, когда функция распределения 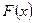— ступенчатая функция. При этом возможные значения — точки 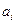скачков 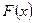, и 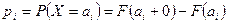— величины скачков.