Примеры абсолютно непрерывных распределений

Опр. Случайная величина имеет абсолютно непрерывное распределение, если существует неотрицательная функция 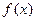такая, что для любого 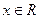функция распределения 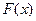представима в виде

.

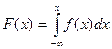Равномерное.

Пример. Будем говорить, что случайная величина имеет равномерное распределение на отрезке 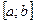и писать 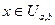, если — координата точки, брошенной наудачу на отрезок 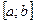числовой прямой. Это распределение можно задать и с помощью функции распределения:

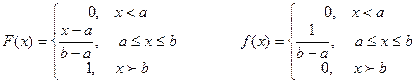
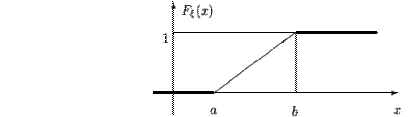
Заметим, что в точках 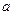и 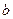функция распределения не дифференцируема, и плотность можно задать как угодно.