2015-06-10
612
Пусть известно статистическое распределение частот количественного признака 
. Введем обозначения: 
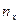- число наблюдений, при которых наблюдалось значение признака, меньшее 
; 
- общее число наблюдений (объем выборки).
Очевидно, что относительная частота события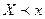 
равна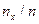 
- это есть функция от . Так как эта функция находится опытным (эмпирическим) путем, то ее называют эмпирической.
Опр. Эмпирической функцией распределения (ЭФР)называют функцию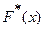 
, определяющую для каждого значения относительную частоту события .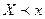
,
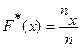где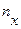 
- число вариант, меньших ; - объем выборки.
Различие между ЭФР и теоретической функциями состоит в том, что теоретическая функция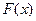 
определяет вероятность события 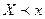, а ЭФР 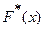определяет относительную частоту этого же события.
Свойства эмпирической функции распределения.
1. Значения функции распределения принадлежат отрезку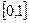 
:
.
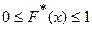2. 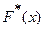- неубывающая функция;
3. Если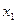 
- наименьшая варианта, а 
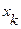- наибольшая варианта, то:
.
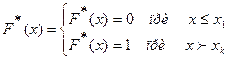График ЭФР – прерывная ступенчатая линия, скачки которой соответствуют наблюдаемым значениям СВ и по величине равны частотам этих значений.
Итак, ЭФР выборки служит для оценки теоретической функции распределения генеральной совокупности.
