Числовые характеристики статистического распределения

Для статистических распределений существуют аналогичные распределениям СВ числовые характеристики.

Пусть имеется СВ , наблюдаемые значения которой .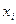

Аналогией МО СВ является среднее арифметическое наблюдаемых значений СВ, т.е. выборочная (статистическая) средняя:

,

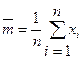где 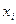- значение СВ, наблюдаемое в 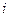-м опыте, - число опытов.

Аналогией дисперсии СВ является выборочная (статистическая) дисперсия:

,

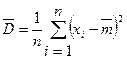где 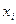- значение СВ, наблюдаемое в 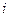-м опыте, - число опытов.

Для практики более удобна формула

. (*)

► ◄

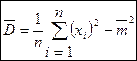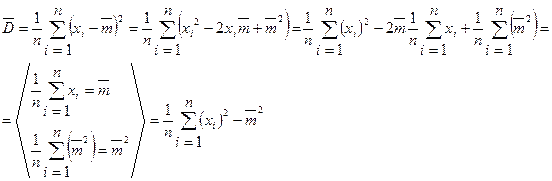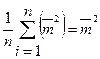так как наблюдаемые значения 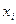рассматриваем как СВ, каждая из которых распределена по тому же закону, что и СВ (тема: одинаково распределенные СВ).

Аналогично определяются статистические начальные и центральные моменты любых порядков:

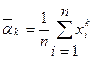и .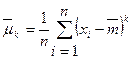

Заметим, что при увеличении все статистические характеристики будут сходиться по вероятности к соответствующим числовым характеристикам СВ и при достаточно большом могут быть приняты приближенно равными им.

Различают генеральные и выборочные числовые характеристики. Если изучается вся генеральная совокупность объема 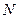относительно некоторого количественного признака , то характеристики генеральные. Если же изучается выборка объема из генеральной совокупности, то характеристики выборочные.

Так для дискретной генеральной совокупности:

Генеральной средней 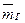называют среднее арифметическое значений признака генеральной совокупности.

Причем, если все значения 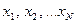признака различны, то

,

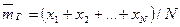если же значения признака имеют частоты 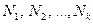, причем 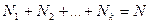, то

.

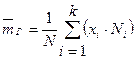Заметим, что если рассматривать обследуемый признак генеральной совокупности как СВ, то

.

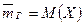Для генеральной совокупности с непрерывным распределением признака также .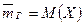

Выборочной средней 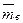называют среднее арифметическое значение признака выборочной совокупности.

Если все значения 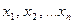признака выборки объема различны, то

.

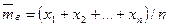Если же значения 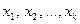признака имеют соответственно частоты 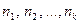, причем 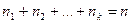, то

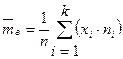, (1)

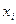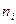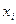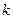где - варианта выборки, - частота варианты , - объем выборки, - количество интервалов.

При построении группированного ряда, учитывая что 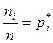, из (1) имеем:

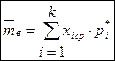, (2)

где 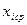- среднее значение варианты на каждом интервале.

Генеральной дисперсией 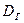называют среднее арифметическое квадратов отклонений значений признака ГС от их среднего значения .

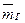Если все значения 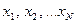признака ГС объема 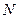различны, то

.

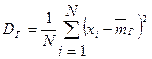Если же значения признака имеют частоты 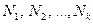, причем 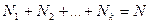, то

.

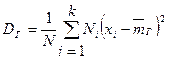Выборочной дисперсией 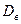называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .

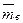Если все значения 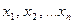признака выборки объема различны, то

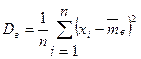или из (*): .

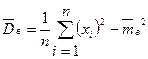Если же значения 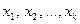признака имеют соответственно частоты 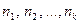, причем 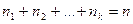, то

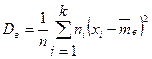. (3)

Корень квадратный из выборочной дисперсии называется выборочным средним квадратическим отклонением.

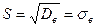(4)