Эмпирическая ф-ция распределения и ее св-ва

Опр.: эмпирической ф-цией распр. называется относ. частота события {X<x} в данной выборке знач. СВ Х, т.е. 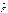(x) = P(X<x) = m_x/n, где m_x – число x_i, меньших х; n – объем выборки. Вел-на n 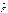(x) равна числу элементов выборки, которые меньше х. Из т. Бернулли следует, что эмпирическая ф-ция 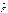(x) при увеличении n (n→∞) сходится по вероятности к подлинной ф-ции распр. F(x). Поэтому 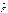(x) используется для оценки ф-ции распр. F(x). Св-ва эмпирической ф-ции распр.: 1) Знач. эмпирич. ф-ции распр. принадлежат отрезку [0;1]; 2) Эмпирич. ф-ция распр. 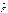(x) – неубывающая ф-ция; 3) Если x< x₁, где x₁ – наименьшее наблюденное значение, то 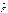(x) = 0; при x> x_n, где x_n – наибольшее наблюденное значение, 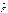(x) = 1. Эти св-ва следуют из определения эмпирической ф-ции распр..