Понятие о теореме Ляпунова

Если Х1, Х2, …, Хn,… - независимые случ. вел-ны, имеющие один и тот же закон распр. с мат. ожиданием m и дисперсией σ 2, то при неограниченном увеличении n закон распр. суммы 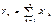неограниченно приближается к нормальному. Док-во: Приведем док-во для случая непрерывных СВ Х1, Х2, …, Хn, кот. имеют один и тот же закон распр. с плотностью f(x) и, следовательно, одну и ту же характеристическую функцию 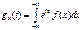- формула (1). (Характеристической ф-цией СВ Х называется ф-ция g(t)=M[eitx], где i – мнимая единица). Исследуем более подробно функцию gx(t). gx(t) = gx(0) + g'x(0)t + [g''x(0)/2+α(t)]t2, где α(t)→0 при t→0 – формула (2). Найдем вел-ны gx(0), g'x(0), g''x(0). Полагая в формуле (1) t=0, имеем: gx(0) = 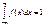. Продифференцируем формулу (1) по t: g'x(0) = 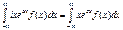- формула (3). Полагая, что в формуле (3) t=0, имеем: g'x(0) = i 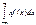= iM[X] = im. Продифференцируем формулу (3): g''x(t) = 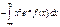, отсюда g''x(0) = 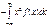- формула (4). При m=0 интеграл в выражении (4) есть не что иное, как дисперсия вел-ны Х с плотностью f(x), следоват-но: g''x(0) = — σ 2. Подставляя в формулу (2) gx(0) = 1, g'x(0) = 0, g''x(0) = — σ 2, получим: gx(t) = 1 – [σ 2/2 - α(t)]t2 – формула (5). Обратимся к СВ Yn. Мы хотим доказать, что ее закон распр. при увеличении n приближается к нормальному. Для этого перейдем от вел-ны Yn к другой СВ: 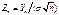- формула (6). Эта вел-на удобна тем, что ее дисперсия не зависит от n и равна 1 при любом n. Если мы докажем, что закон распр. вел-ны Zn приближается к нормальному, то, очевидно, это будет справедливо и для вел-ны Yn, связанной с Zn линейной зависимостью. Из формулы (6): gzn(t)=gyn(t/σ 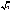), где gyn(t) – характеристическая ф-ция СВ Yn. Из формулы (5): gzn(t) = {1- [σ 2/2 – α(t/σ 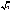)] (t2 /n σ 2)}n. Прологарифмируем это выражение: ln gzn(t) =n ln {1- [σ 2/2 – α(t/σ 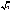)] (t2 /n σ 2)}. Введем обозначение [σ 2/2 – α(t/σ 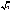)] (t2 /n σ 2) = χ. Тогда ln gzn(t) =n ln{1- χ}. Будем неограниченно увеличивать n. При этом вел-на χ стремится к 0. Разложим ln{1- χ} в ряд и ограничимся одним членом разложения: ln{1- χ} = — χ. Тогда получим 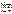ln gzn(t) = 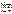n(— χ) = 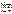{ - t 2/2 + α(t/σ 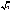)] (t2 / σ 2)} = - t 2/2 + 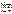(t2 / σ 2) α(t/σ 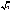). Ф-ция α(t) стремится к 0 при t→0; значит 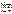α(t/σ 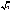) = 0 и 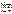ln gzn(t) = (- t 2/2), откуда 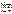gzn(t) = 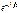. Это есть не что иное, как характеристическая ф-ция нормального закона с параметрами m=0, σ =1. Т.о. доказано, что при увеличении n характирестич. ф-ция СВ Zn неограниченно приближается к характ. ф-ции нормального закона; отсюда – закон распр. вел-ны Zn, а значит и вел-ны Yn, неограниченно приближается к нормальн. закону. Теорема доказана.