Проверяя гипотезы (Г.) с помощью стат. критерия, может возникнуть одна из четырех ситуаций: 1) Г. H0 истинна (и поэтому H1 – ложна) и предпринимается действие А; 2) Г. H1 истинна (и поэтому H0 – ложна) и предпринимается действие А; 3)) Г. H0 истинна (и поэтому H1 – ложна) и предпринимается действие В; 4) Г. H1 истинна (и поэтому H0 – ложна) и предпринимается действие В. В ситуациях 2 и 3 получается ошибка. Существует 2 типа ошибок. Ошибка, состоящая в принятии Г. H0, когда она ложна (ошибка второго рода), качественно отличается от ошибки, состоящей в отвержении H0, когда она истинна (ошибка первого рода). При этом числа αi = αi(δ) = Pi(δ(X)≠ Hi), характеризующие вер. отвержения Г. Hi, когда она верна, называют вер-ми ошибок (i+1)-го рода критерия δ. Набором вер. αi(δ) ошибочных решений хар-ся кач-вом критерия δ. Правильное решение также может быть принято двумя способами (ситуации 1 и 4): когда Г. H0 принимается, ибо она верна, и когда Г. H0 отвергается, ибо она ложна. В ситуации 1 не совершается ошибка первого рода, в ситуации 4 – второго рода. Уровень значимости критерия не меняет степени риска, связанного с возможностью ошибки второго рода, т.е. с принятием неверной Г.. И при данном уровне значимости можно по-разному определить критическую область. Как правило, ее определяют так, чтобы мощность критерия 1 – α1(δ) была возможно большей: P (X 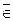 ] x1; x2[|H1) = max. Мощностью критерия δ называется вер. 1 – α1(δ) несовершения ошибки второго рода. Чем больше мощность критерия, тем меньше вер. принятия неверной Г.
] x1; x2[|H1) = max. Мощностью критерия δ называется вер. 1 – α1(δ) несовершения ошибки второго рода. Чем больше мощность критерия, тем меньше вер. принятия неверной Г.
???? Вер. отклонения относит. частоты от постоян. вер. в независим. испытаниях. Будем считать, что производится n независ. испытаний, в кажд. из кот. вер. появл. соб. А постоянна и равна p. Найдем вер. того, что отклонение относит. частоты 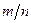 от постоян вер. p по абсолютн. величине не превышает задан. числа
от постоян вер. p по абсолютн. величине не превышает задан. числа 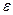 , т.е. найдем вер. осуществления нер-ва:
, т.е. найдем вер. осуществления нер-ва: 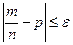 . Заменим дан. нер-во на равносильн. ему нер-во
. Заменим дан. нер-во на равносильн. ему нер-во 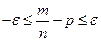 ;
; 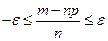 . Умножим последн. нер-во на
. Умножим последн. нер-во на 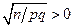 , получим
, получим 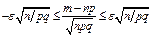 . Воспользуемся интегральн. теоремой Лапл. Положим
. Воспользуемся интегральн. теоремой Лапл. Положим 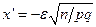 ,а
,а 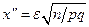 , тогда имеем вер. того, что P(
, тогда имеем вер. того, что P(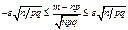 )
) 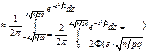 . Окончательно получаем
. Окончательно получаем 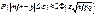
 2015-06-10
2015-06-10 756
756








