Теорема Чебышева или закон больших чисел в форме Чебышева
Напомним, что если 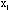 ,
, 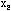 ,…,
,…, 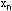 попарно независимые случайные величины, имеющие М(х
попарно независимые случайные величины, имеющие М(х  ) и D(х
) и D(х  ), i=1,n, то для новой случайной величины
), i=1,n, то для новой случайной величины 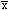 =
= 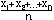 или
или 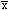 =
= 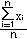 справедливо нер-во
справедливо нер-во
М(х)= 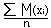
Последовательность а1,а2,..,аn называется равномерно ограниченной, если |ai| 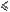 c, где c-константа, не зависит от i.
c, где c-константа, не зависит от i.
Теорема: При неограниченном увеличении числа n попарно независым. случ. вел-е, имеющегося мат осн-я и равн-но ограниченной дисперсии, их ср арифметическая 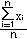
стремится по вертикали к ср арифметическому их мат ожидания,т.е. к 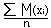
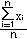 à
à 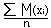
Доказательство:
Следствие1: Если случ вел-ны 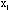 ,
, 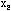 ,…,
,…, 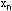 имеют равный математические ожилпния М(х
имеют равный математические ожилпния М(х  )=а и равно ограничены дисперсии D(х
)=а и равно ограничены дисперсии D(х  ),то
),то 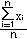 àa за истинное значение измеряемой вел-ны берут ср арифметическую большого числа ее изм-ий.
àa за истинное значение измеряемой вел-ны берут ср арифметическую большого числа ее изм-ий.
Следствие2: Теорема Хинчина: Если с.в. х  имеют одинаковое расп-е, т.е. М(х
имеют одинаковое расп-е, т.е. М(х  )=а и D(х
)=а и D(х  )=r^2, то для всех i
)=r^2, то для всех i 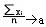
 2015-06-10
2015-06-10 195
195








