2015-06-10
410
Т еорема. Пусть производится n независимых опытов, в каждом из которых вероятность наступления события А одна и та же и равна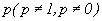 
. Пусть m - число появления события A в n опытах. Тогда для достаточно больших n случайная величина m имеет распределение, близкое к нормальному с параметрами a=M(m)=np,
Доказательство. Пусть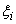 
- число наступления события A в i -м опыте. Тогда 
, 
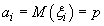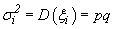(cм. § 4, п. 2, пример 2). Так как 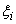может принимать только два значения 0 и 1, то для любого i имеем 
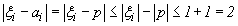. Кроме того, величина 
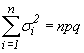стремится к бесконечности при 
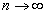. Итак, последовательность случайных величин 
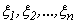удовлетворяет условиям следствия из теоремы Ляпунова. Поэтому сумма этих величин 
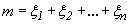достаточно больших n имеет распределение, близкое к нормальному, что и требовалось доказать.
Вычислим вероятность того, что случайная величина m, т. е. число наступлений события А в n опытах, удовлетворяет неравенствам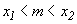 
, где x1 и x2 - данные числа. Так как a=M(m)=np, 
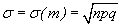(cм. § 4, п. 2, пример 2). То согласно формуле (32) получим
|
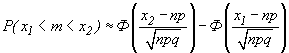
где Ф(х) - интеграл вероятностей.
|
|
|
