Пусть дана случайная величина 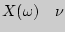 а
а 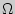 . Если ряд
. Если ряд 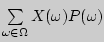 сходится абсолютно, то его сумма
сходится абсолютно, то его сумма 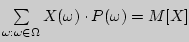 называется математическим ожиданием (м.о.) с.в.
называется математическим ожиданием (м.о.) с.в. 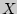 .
.
Свойства математического ожидания:
1. 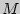 [
[ 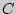 ] =
] = 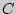 , где
, где 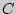 - const;
- const;
2. 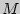 [
[  ] =
] =  [
[ 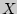 ];
];
3. 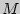 [ X
[ X 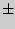 Y ] =
Y ] = 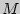 [
[ 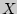 ]
] 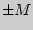 [
[ 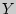 ];
];
4. 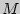 [ X
[ X  Y ] =
Y ] = 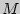 [
[ 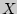 ]
] 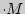 [
[ 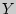 ], где
], где 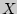 и
и 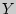 - независимые с.в.
- независимые с.в.
Случайные величины 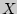 и
и 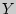 называются независимыми, если для любых
называются независимыми, если для любых 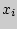 ,
, 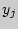 имеет место равенство
имеет место равенство 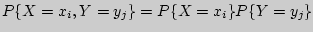 .
.
Модой 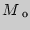 д.с.в. называется ее наиболее вероятное значение.
д.с.в. называется ее наиболее вероятное значение.
Медианой 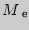 ряда значений
ряда значений 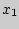 <
< 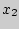 <...<
<...< 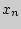 , которые с.в.
, которые с.в. 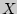 принимает с вероятностями
принимает с вероятностями 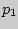 ,
, 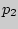 ,...,
,..., 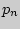 соответственно, называется значение
соответственно, называется значение 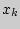 с таким индексом
с таким индексом 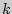 , что
, что 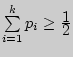 и
и 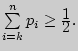 Это означает, что приблизительно одинаково вероятно, продолжится ли процесс после медианы или закончится до нее.
Это означает, что приблизительно одинаково вероятно, продолжится ли процесс после медианы или закончится до нее.
Если математическое ожидание с.в. 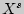 существует, то оно называется начальным моментом
существует, то оно называется начальным моментом 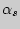 [
[ 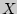 ] порядка
] порядка 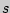 с.в.
с.в. 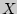 :
:
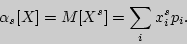
Поскольку 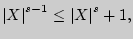 то из существования
то из существования 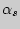 [
[ 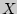 ] вытекает существование
] вытекает существование 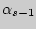 [
[ 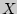 ] и, следовательно, существование всех начальных моментов порядка меньше
] и, следовательно, существование всех начальных моментов порядка меньше 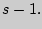
Математическое ожидание с.в. является ее первым начальным моментом:
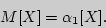
Начальные моменты, мода и медиана являются характеристиками положения случайной величины.
Начальный момент 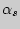 [
[ 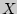 ] д.с.в. можно находить как вес всего графа распределения с.в.
] д.с.в. можно находить как вес всего графа распределения с.в. 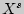 :
:
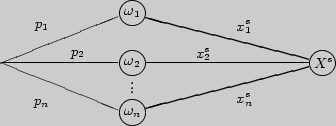
Рис. 47
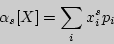
Понятие математического ожидания случайной величины ввели в середине XVIIв. Гюйгенс и Схоутен.
 2015-06-10
2015-06-10 361
361








