2015-06-10
267
Важным приложением закона Пуассона является рассмотрение случая, когда событие А в n испытаниях не произойдет ни разу, т.е. в формуле (3.8) имеем К = 0. При этом указанная формула примет вид:
Pn = e-a. (3.9)
Представим параметр a как число отказов за промежуток времени t:
a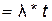 
, (3.10)
где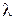 
- число (интенсивность) событий А в единицу времени.
Тогда вероятность ненаступления события А в течение некоторого промежутка времени t описывается показательным распределением вероятностей, которое имеет вид:
функция распределения -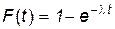 
;
плотность распределения -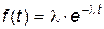 
, (3.11)
где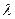 
- постоянная положительная величина
Показательное распределение характеризуется только одним параметром .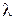
Примером распределения по показательному закону может служить время между появлениями двух последовательных событий (например, отказов, т.е. нарушений предельного состояния).
Вероятность попадания в заданный интервал показательно распределенной случайной величины равна:
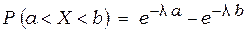. (3.12)
Функция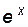 
- табулирована.
Числовые характеристики показательного распределения:
|
|
|
; 
; 
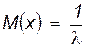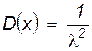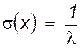. (3.13)
