Вероятность события в современном построении курса определяется аксиоматически (аксиоматическая структура теории вероятностей была предложена советским математиком А. Н. Колмогоровым в 1933 году). Дадим это определение в упрощенной трактовке.
Пусть 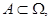 т. е. событие
т. е. событие 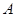 образовано из каких-нибудь исходов пространства элементарных событий некоторого испытания. Числовая функция
образовано из каких-нибудь исходов пространства элементарных событий некоторого испытания. Числовая функция 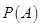 , определенная на множестве всех событий этого испытания, называется вероятностью события
, определенная на множестве всех событий этого испытания, называется вероятностью события 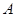 , если она удовлетворяет следующим аксиомам:
, если она удовлетворяет следующим аксиомам:
Аксиома 1: 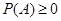 .
.
Аксиома 2: вероятность достоверного события 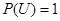 .
.
Аксиома 3: если 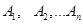 попарно несовместные события, то
попарно несовместные события, то
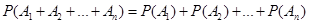 – вероятность суммы несовместных событий равна сумме вероятностей этих событий.
– вероятность суммы несовместных событий равна сумме вероятностей этих событий.
В аксиоматическом определении свойства вероятности, справедливые для испытаний с равновозможными исходами, обобщены на случай произвольных испытаний. Эти свойства, в общем случае, ниоткуда не следуют, они постулируются. Именно так, с помощью некоторого набора аксиом, определяются исходные понятия в современной математике.
Можно показать, что «классическое определение» вероятности (3.4) получается как частный случай аксиоматического определения, если исходы испытания равновероятны,
Без доказательства приведем несколько следствий из аксиом 1–3:
1. 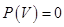 , (
, (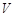 – невозможное событие).
– невозможное событие).
2. Если 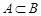 , то
, то 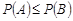 .
.
3. 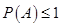 , (вместе с аксиомой 1 имеем
, (вместе с аксиомой 1 имеем 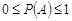 ).
).
4. Если исходы 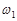 ,
, 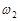 , …,
, …, 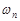 образуют пространство элементарных событий, то
образуют пространство элементарных событий, то 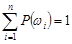 .
.
5. 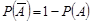 .
.
 2015-06-10
2015-06-10 633
633








