Случайные процессы и шумы описываются функциями автокорреляции и спектрами мощности. Модели случайных процессов (сигналов) с заданными статистическими характеристиками обычно получают фильтрацией белого шума.
Белый шум является стационарным случайным процессом q(t), у которого автокорреляционная функция описывается дельта - функцией Дирака и, соответственно, спектральная плотность мощности не зависит от частоты и имеет постоянное значение Wq(f) = s2, равное дисперсии значений q(t). Другими словами, все спектральные составляющие белого шума имеют одинаковую мощность (как белый цвет содержит все цвета видимого спектра). По существу, это идеализированный случайный процесс с бесконечной энергией. Но в случае постоянства спектральной плотности мощности случайного процесса в конечном диапазоне частот введение такой идеализации позволяет разрабатывать достаточно легко реализуемые оптимальные методы фильтрации. Многие помехи в радиотехнике, в технике связи и в других отраслях, в том числе в информатике, рассматривают как белый шум, если эффективная ширина спектра сигналов Bs много меньше эффективной ширины спектра шумов Bq, а спектральная плотность мощности шумов слабо изменяется в интервале спектра сигнала. Понятие "белый шум" определяет только спектральную характеристику случайного процесса и под это понятие подпадают любые случайные процессы, имеющие равномерный энергетический спектр и различные законы распределения.
Если частотный диапазон спектра, на котором рассматриваются сигналы и помехи, равен 0-В, то спектральная плотность шума задается в виде:
Wq(f)=s2, 0£ f £B; Wq(f)=0, f > B, (12.1.1)
при этом корреляционная функция шума определяется выражением:
Rq(t)= s2 B×sin(2pBt)/2pBt. (12.1.2)
Эффективный интервал корреляции:
Tk = 2 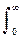 |Rq(t)|dt /Rq(0). (12.1.3)
|Rq(t)|dt /Rq(0). (12.1.3)
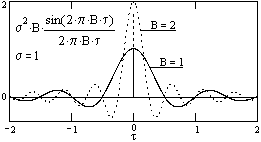 Рис. 12.1.1. Функции корреляции белого шума в частотном интервале 0-В. Рис. 12.1.1. Функции корреляции белого шума в частотном интервале 0-В. |
Реальный интервал корреляции целесообразно определять по ширине главного максимума функции Rq(t) (значения t при первых пересечениях нулевой линии), в котором сосредоточена основная часть энергии шумов, при этом Tk = 1/В и BTk = 1.
Как следует из всех этих выражений и наглядно видно на рис. 12.1.1, при ограничении частотного диапазона в шумах появляется определенная корреляция между значениями, и, чем меньше частотный диапазон шумов, тем больше их радиус корреляции. По существу, ограничение шумов определенным частотным диапазоном эквивалентно фильтрации белого шума частотным фильтром с соответствующей шириной полосы пропускания, при этом, корреляционная функция импульсного отклика фильтра свертывается с дельта – функцией белого шума.
Модель белого шума q(t) можно формировать как случайную по времени (аргументу) последовательность дельта - импульсов d(ti) со случайными амплитудными значениями ai:
q(t) = Si ai d(t-ti), (12.1.4)
которая удовлетворяет условиям статистической однородности: постоянное среднее число импульсов в единицу времени и статистическая независимость появления каждого импульса от предыдущих. Такой поток импульсов, который называют пуассоновским, является некоррелированным и имеет равномерный спектр плотности мощности:
Wq(w) = c2 = Nsa2,
где N - число импульсов на интервале Т реализации случайного процесса, sa2 -дисперсия амплитуд импульсов.
Фильтрация белого шума. Спектральное описание белого шума оказывается удобным при учете влияния на него амплитудно-частотных характеристик различных устройств. Если на входе фильтра с импульсным откликом h(t) действует белый шум q(t), то сигнал на выходе фильтра:
g(t) = h(t) ③ q(t) = h(t) ③ Si ai d(t-ti) =Si ai h(t-ti), (12.1.5)
т.е. выходной сигнал будет представлять собой последовательность сигналов импульсной реакции фильтра h(t) с амплитудой ai, при этом автокорреляционная функция и спектр мощности выходного потока также становятся подобными ФАК и спектру мощности импульсной реакции фильтра, и в первом приближении определяются выражениями:
Rg(t) 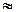 N sa2 Rh(t) = c2 Rh(t), (12.1.6)
N sa2 Rh(t) = c2 Rh(t), (12.1.6)
Wg(w) 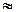 N sa2 |H(w)|2 = c2 |H(w)|2. (12.1.7)
N sa2 |H(w)|2 = c2 |H(w)|2. (12.1.7)
Этот результат известен как теорема Кэмпбелла.
Курсовая работа 23-07. Исследование и разработка методики и программы оценки шумов малошумящих датчиков, подключенных на вход усилителей.
 2015-06-10
2015-06-10 738
738








