Общий порядок решения задач методом динамического программирования при конечном числе состояний управляемого объекта

1. Примем следующие условные обозначения: S – управляемый объект (система); 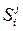- управляемый объект на i-м этапе в j-м состоянии; U – управление; 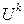(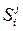)® 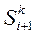- управление, переводящее объект S из j-го состояния на i-м этапе в k-состояние на (i+1)-м этапе; W[ 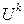(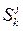)] - выигрыш от управления 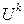(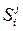); S₀ – начальное состояние объекта; 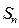- конечное состояние объекта.

2. Решение начинается с расчленения задачи на этапы так, чтобы объект S, находящийся в одном из состояний на i-м этапе (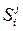), переводился в некое состояние k на (i+1)-м этапе альтернативными управлениями 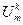, каждое из которых можно распознать (т.е. отличить друг от друга) и характеризовать выигрышем. Иными словами, выигрыш от управления должен быть легковычисляемым. В частных случаях m может равняться единице, что означает отсутствие возможности выбора (альтернативы) управлений.

3. Начинают расчеты с последнего n-го этапа. Не зная еще оптимального управления, которое приведет объект S₀ в 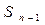, будем исходить из того, что на этапе n-1 объект S может находиться в любом из состояний, присущих этому этапу. Выпишем в особую таблицу все управления, переводящие 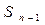в 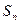и заметим выигрыши, которые им соответствуют. Все необходимые записи удобнее сделать на графе, изображающем этапы процесса решения и состояния объекта.

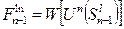
4. Переходим к расчетам на этапе n-1. Пусть на этапе n-2 объект S может находиться в j-х состояниях, а на этапе n-1 в l-х состояниях и существует k управлений, переводящих 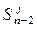в 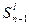. Как и в предыдущем случае, нам еще не известно оптимальное управление, переводящее S₀ в 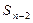, т.е. мы еще не знаем, какое значение соответствует этому оптимальному управлению. Фиксируем по очереди номер и для каждого j ищем максимум следующего функционального выражения:

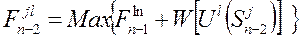
Эта не очень привычная для читателей символическая запись означает следующее: на этапе n-2 рассматриваем состояние j и состояние l, в которые может перейти 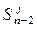, на этапе n-1; рассчитываем выигрыши от управлений, переводящих 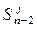в 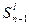для разных l, складываем эти выигрыши с ранее зафиксированным выигрышем 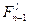от управления, переводящего 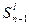в 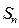; выбираем такой номер l состояния 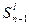, чтобы соответствующая сумма была максимальной. Обозначим ее символом 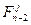; фиксируем управление, обеспечивающее эту максимальную сумму выигрышей; те же действия проделываем для каждого j.

5. Полученные числа и соответствующие им управления записываем в таблицу или отображаем на графе.

6. Переходим к этапу n-3 и проделываем все действия по пунктам 4 и 5.

7. Дойдя до начального состояния S₀, выбираем, ориентируясь на числа 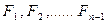и соответствующие им управления, такую последовательность управлений, которым на каждом этапе соответствуют:

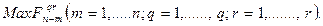
Такой набор управлений по этапам соответствует максимальному выигрышу и, следовательно, является оптимальным.

Надо учесть, что студенту, только начинающему изучать сущность динамического программирования, это общее и довольно абстрактное описание порядка решения еще не дает в руки практического способа применения метода для решения задач. Тем не менее, ему рекомендуется затратить усилия для уяснения именно общих принципов решения, ибо каждая конкретная задача может решаться с некоторыми отступлениями от указанного порядка, если эти отступления несколько сократят объект вычислений. Но общие принципы нарушаться при этом не должны.

В пункте 4 одно из действий предписывало суммировать выигрыши на последнем и предпоследнем этапах, а пункт 6 предусматривает, что подобные суммирования будут иметь место и в дальнейшем. Так действуют, е с л и критерий эффективности а д д и т и в е н. Следовательно, при выборе критерия надо позаботиться о том, чтобы он соответствовал этому требованию. Если, например, выбран такой критерий, как отношение прибыли к убыткам, то хотя он и может быть вычислен для каждого этапа, суммировать его по этапам нельзя: он не отвечает требованию аддитивности.

Если объект приведен в состояние 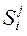, то оптимальный выигрыш для управлений, переводящих 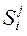в состояние 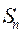, не з а в и с и т от того, каким образом объект S доведен до состояния 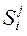, т.е. не зависит от предыстории, от прошлого. При решении задач о распределении ассигнований между судами тралового флота и океанического рыболовства по годам считается, что в первый год экономический эффект от этих ассигнований пропорционален (с соответствующими коэффициентами) массе вкладываемых средств, то на второй год эти коэффициенты изменятся в з а в и с и м о с т и от р а с п р е д е л е н и я ассигнований за п р е д ы д у щ и й год. Существует метод, позволяющий обойти это препятствие для применения динамического программирования, но это можно сделать только за счет усложнения задачи и увеличения объема вычислительных работ.

Поэтому, перед решением задачи методом динамического программирования с выбранным критерием эффективности, нужно проверить, выполняется ли для задачи следующее условие, или, как его иногда называют, принцип оптимальности, включающий в себя оба разобранных ограничения: аддитивность критерия эффективности и независимость от предыстории.

Уточним пункт 4. Что представляют собой 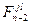и соответствующие им управления? Они получены в предложении, что если на этапе n-2 объект будет приведен предшествующими управлениями в состояние j, то 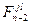и управление, ему соответствующее, представляют оптимальный выигрыш и оптимальное управление на последующих этапах. Наличие логической связки «если, то» позволяет назвать их условными оптимальными выигрышами и у с л о в н ы м и оптимальными управлениями. Их вычисление означает, что мы просто-напросто используем принцип оптимальности, обеспечивая о п т и м а л ь н о е п р о д о л ж е н и е п р о ц е с с а относительно достигнутого в данный момент состояния.

Является ли достигнутое в данный момент состояние результатом оптимального управления в прошлом или оно есть следствие управлений, и близко не похожих на оптимальные, мы не знаем. И не узнаем до тех пор, пока не закончим подсчеты условных оптимальных управлений с конца до начала. Но, дойдя до начала, мы опять должны двинуться к концу, выбирая на этот раз уже безусловные оптимальные управления, так как исходное состояние объекта S₀ нам было задано. Если при движении от конца к началу требовалось выполнять множество вычислений, то при движении от начала к концу нам только остается «собирать по пути» оптимальные управления на каждом этапе.