Введенная терминология и доказанные утверждения позволяют ответить на вопрос о совместности произвольных систем линейных уравнений (теперь уже не ограничиваемся предположением, что число уравнений равно числу неизвестных)
 (1)
(1)
Рассмотрим расширенную матрицу этой системы

Теорема Кронекера – Капелли: Система линейных уравнений тогда и только тогда совместна, когда ранг расширенной матрицы равен рангу матрицы A.
Действительно, пусть k 1, k 2,..., k n, будет одним из ее решений. Подставляя ее в систему (1) получаем s тождеств. Значит, последний столбец расширенной матрицы является линейной комбинацией остальных столбцов с этими коэффициентами. Всякий другой столбец этой матрицы также является линейной комбинацией других столбцов. Отсюда следует, что столбцы матрицы A и ее расширенной матрицы 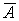 эквивалентны между собой, а потому имеют один и тот же ранг.
эквивалентны между собой, а потому имеют один и тот же ранг.
Пусть теперь дано, что матрица A и расширенная матрица имеют одинаковые ранги. Тогда любая максимальная линейно независимая система столбцов матрицы A остается максимальной линейно независимой системой столбцов и в расширенной матрице 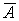 . Таким образом, через эту систему, а поэтому и вообще через систему столбцов матрицы A линейно выражается последний столбец расширенной матрицы. Значит, коэффициенты линейной зависимости k 1, k 2,..., k n составляют решение системы (1). Таким образом, совпадение рангов матриц A и расширенной матрицы
. Таким образом, через эту систему, а поэтому и вообще через систему столбцов матрицы A линейно выражается последний столбец расширенной матрицы. Значит, коэффициенты линейной зависимости k 1, k 2,..., k n составляют решение системы (1). Таким образом, совпадение рангов матриц A и расширенной матрицы 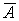 влечет за собой совместность системы (1).
влечет за собой совместность системы (1).
ð
Теорема полностью доказана. При ее применении к конкретным примерам следует сперва вычислить ранг матрицы A. Для этого надо найти один из тех отличных от нуля миноров этой матрицы, что все миноры, его окаймляющие равны нулю – пусть это будет минор M. После этого следует вычислить все миноры, окаймляющие M, но в A не содержащиеся (так называемые характеристические определители системы). Если все они равны нулю, то ранг матрицы 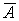 равен рангу матрицы A и потому система (1) совместна, в противном случае она не совместна. Таким образом, теореме Кронекера-Капелли можно дать такую формулировку: система линейных уравнений (1) тогда и только тогда совместна, если все ее характеристические определители равны нулю.
равен рангу матрицы A и потому система (1) совместна, в противном случае она не совместна. Таким образом, теореме Кронекера-Капелли можно дать такую формулировку: система линейных уравнений (1) тогда и только тогда совместна, если все ее характеристические определители равны нулю.
Предположим теперь, что система (1) совместна. Обратимся к задаче практического разыскания всех решений системы.
Пусть матрица A имеет ранг r, т. е. максимальное число линейно независимых строк матрицы A равно r. Пусть для определенности это будут первые r сток. Из совпадения рангов матриц A и 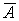 следует, что первые r строк матрицы
следует, что первые r строк матрицы 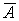 составляют в ней максимальную линейно независимую систему строк.
составляют в ней максимальную линейно независимую систему строк.
Отсюда следует, что всякое уравнение системы (1) можно представить как сумму первых r уравнений, взятых с некоторыми коэффициентами, а потому любое общее решение первых r уравнений будет удовлетворять всем уравнениям системы (1). Достаточно, следовательно, найти все решения системы
 (2)
(2)
Матрица (2) имеет ранг r, r £ n, кроме того, хотя бы один из миноров r -го порядка отличен от нуля. Если r = n то (2) будет системой с равным числом уравнений и неизвестных и с отличным от нуля определителем. Тогда она, а потому и система (1) обладает единственным решением.
Пусть теперь r < n и пусть, для определенности, отличен от нуля минор r -го порядка, составленный из коэффициентов при первых r неизвестных. Перенесем в каждом из уравнений (2) в правую часть все члены с неизвестными x 1, x 2,..., x n и выберем для этих неизвестных некоторые значения c 1, c 2,..., c n. Мы получим систему r уравнений
 (3)
(3)
относительно r неизвестных x 1, x 2,..., x r. К этой системе применимо правило Крамера и поэтому она обладает единственным решением c 1, c 2,..., c r; очевидно, что система чисел c 1, c 2,..., c r, c r+1,..., c n будет служить решением системы (2). Так как значения c r+1,..., c n для неизвестных x r+1,..., x n, называемых свободными неизвестными выбраны произвольным образом, то этим путем получается бесконечно много различных решений системы (2).
С другой стороны, если дано некоторое решение c 1, c 2,..., c n системы (2), то в качестве значений для свободных неизвестных берем числа c r+1,..., c n. Тогда числа c 1, c 2,..., c r будут удовлетворять системе (3) и поэтому будут составлять то единственное решение этой системы, которое вычисляется по правилу Крамера.
Из изложенного выше следует следующее правило решения произвольной системы линейных уравнений:
Пусть дана совместная система линейных уравнений (1) и пусть матрица из коэффициентов A имеет ранг r. Выбираем в A r линейно независимых строк и оставляем в системе лишь уравнения, коэффициенты которых вошли в выбранные строки. В этих уравнениях оставляем в левых частях такие r неизвестных, что определитель из коэффициентов при них отличен от нуля, а остальные неизвестные объявляем свободными и переносим в правые уравнений. Давая свободным неизвестным произвольные числовые значения и вычисляя значения остальных неизвестных по правилу Крамера, получаем все решения системы (1).
Дополнительно еще раз формулируем полученный результат:
Совместная система тогда и только тогда обладает единственным решением, если ранг матрицы равен числу неизвестных.
Примеры:
1. Решить систему
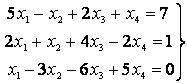
Ранг матрицы из коэффициентов равен двум: минор второго порядка, стоящий в левом верхнем углу этой матрицы, отличен от нуля, но оба минора третьего порядка, его окаймляющие, равны нулю. Ранг расширенной матрицы равен трем, так как
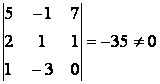
Отсюда следует, что система несовместна.
2. Решить систему
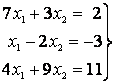
Ранг этой матрицы из коэффициентов равен двум, т. е. равен числу неизвестных; ранг расширенной матрицы тоже равен двум. Таким образом, система совместна и обладает единственным решением. Левые части первых двух уравнений линейно независимы; решая эту систему двух уравнений, получим для неизвестных следующие значения:
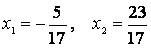
Легко видеть, что это решение удовлетворяет и третьему уравнению.
3. Решить систему

Система совместная, так как ранг расширенной матрицы, как и ранг матрицы из коэффициентов, равен двум. Левые части первого и третьего уравнений линейно независимы, так как коэффициенты при неизвестных x 1 и x 2 составляют отличный от нуля минор второго порядка. Решаем систему из этих двух уравнений, причем неизвестные x 3, x 4, x 5 считаем свободными, переносим в правые части уравнений и предполагаем, что им уже приданы некоторые числовые значения. Мы получим, применяя правило Крамера:

Это равенство определяет общее решение заданной системы. Присваивая в них свободным неизвестным произвольные числовые значения, получим все решения системы. С другой стороны, подставляя выражения для x 1 и x 2 из общего решения в любое уравнение системы, например во второе, ранее исключенное из рассмотрения, получим тождество.
4. Решить систему

Хотя число уравнений равно числу неизвестных, но определитель системы равен нулю и поэтому правило Крамера неприменимо. Ранг матрицы из коэффициентов равен трем – в правом верхнем углу этой матрицы расположен отличный от нуля минор третьего порядка. Ранг расширенной матрицы также равен трем, т. е. система совместна. Рассматривая лишь первые три уравнения и считая неизвестное x 1 свободным, получим общее решение в виде
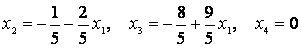
5. Рассмотрим следующую систему.
Пусть она состоит из n +1 уравнений относительно n неизвестных. Расширенная матрица 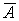 этой системы будет квадратной порядка n +1. Если система совместна, то, по теореме Кронекера–Капелли, определитель матрицы
этой системы будет квадратной порядка n +1. Если система совместна, то, по теореме Кронекера–Капелли, определитель матрицы 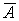 должен быть равным нулю.
должен быть равным нулю.
Так, определитель системы
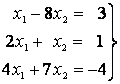
из коэффициентов и свободных членов этих уравнений отличен от нуля:
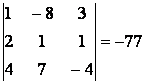
поэтому она не совместна.
Обратное утверждение не будет, вообще говоря, справедливым: из равенства нулю определителя матрицы 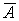 не следует совпадение рангов матриц A и
не следует совпадение рангов матриц A и 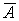 .
.
 2015-06-10
2015-06-10 1991
1991