Системы линейных однородных уравнений

Применим результаты предшествующего параграфа к случаю системы линейных однородных уравнений:

(1)

Из теоремы Кронекера – Капелли вытекает, что эта система всегда совместна, так как добавление столбца из нулей не может повысить ранга матрицы. Это, впрочем, видно и непосредственно – система (1) заведомо обладает нулевым решением (0, 0,..., 0).

Пусть матрица A из коэффициентов системы (1) имеет ранг r. Если n = r, то нулевое решение будет единственным решением системы (1); при r<n система обладает также и решениями, отличными от нулевого.

Заметим, что система из n линейных однородных уравнений с n неизвестными (1) тогда и только тогда обладает решениями, отличными от нулевого, когда определитель этой системы равен нулю. С другой стороны, если в системе однородных уравнений число уравнений меньше числа неизвестных, то система непременно обладает решениями, отличными от нулевого, так как ранг в этом случае не может быть равным числу неизвестных.

Решения систем линейных однородных уравнений, очевидно, обладают следующими, присущими, вообще говоря, только им свойствами. Если вектор b =(b ₁, b ₂,..., b _n) является решением системы (1), то при любом числе k вектор k b =(k b ₁, k b ₂,..., k b_n) также будет решением этой системы. Если, далее, вектор g =(c ₁, c ₂,..., c _n) – еще одно решение системы (1), то для этой системы служит решением и вектор b + g =(b ₁+ c ₁, b ₂+ c ₂,..., b _n+ c _n):

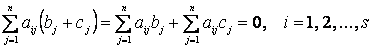
Поэтому вообще всякая линейная комбинация решений однородной системы (1) будет сама решением этой системы.

Мы уже знаем, что всякая система n -мерных векторов, состоящая более чем из n векторов, будет линейно зависимой. Отсюда следует, что из числа решений однородной системы (1), являющихся n -мерными векторами можно выбрать конечную максимальную линейно независимую систему, максимальную в том смысле, что всякое другое решение системы (1) будет линейной комбинацией решений, входящих в эту выбранную систему.

Определение: Всякая максимальная линейно независимая система решений однородной системы уравнений (1) называется ее фундаментальной системой решений.

Еще раз подчеркнем, что n -мерный вектор тогда и только тогда будет решением системы (1), когда он является линейной комбинацией векторов, составляющих данную фундаментальную систему.

Понятно, что фундаментальная система будет существовать лишь в том случае, если система (1) обладает ненулевыми решениями, т. е. если ранг ее матрицы из коэффициентов меньше числа неизвестных. При этом система (1) может обладать многими различными фундаментальными системами решений. Все эти системы эквивалентны между собой и состоят из одного и того же числа решений.

Теорема: Если ранг r матрицы из коэффициентов системы линейных однородных уравнений (1) меньше числа неизвестных n, то всякая фундаментальная система решений системы (1) состоит из n-r решений.

Для доказательства заметим, что n-r является числом свободных неизвестных в системе (1); пусть свободными будут неизвестные x _r+1, x _r+2,…, x _n. Рассмотрим произвольный отличный от нуля определитель d порядка n-r, который запишем в следующем виде:

Беря элементы i -й стоки этого определителя, 1£ i £ n-r, в качестве значений для свободных неизвестных, мы, как известно, получим однозначно определенные значения для неизвестных x ₁, x ₂,..., x _r, т. е. придем к вполне определенному решению системы уравнений (1); запишем это решение в виде вектора

a _i =(c_{i 1}, c_{i 2},..., c_{i r}, c_{i r+1}, c_{i r+2},..., c_{i n})

Полученная система векторов a ₁, a ₂,…, a _n-r, служит для системы уравнений (1) фундаментальной системой решений. В самом деле, эта система векторов линейно независима, так как матрица, составленная из этих векторов как из строк, содержит отличный от нуля минор d порядка n-r. С другой стороны, пусть

b =(b ₁, b ₂,..., b _r, b _r+1, b _r+2,..., b _n)

будет произвольное решение системы (1). Докажем, что вектор b линейно выражается через векторы a ₁, a ₂,…, a _n-r.

Обозначим через 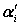, i =1, 2,…, n-r, i -ю строку определителя d, рассматриваемую как (n-r)-мерный вектор. Положим, далее,

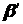=(b _r+1, b _r+2,…, b _n).

Векторы 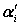, i =1, 2,…, n-r, линейно независимы, так как d ¹0. Однако система (n-r)-мерных векторов

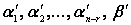
линейно зависима, так как в ней число векторов больше их размерности. Существует, следовательно, такие числа k ₁, k ₂,…, k _n-r, что

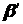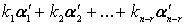= (2)

Рассмотрим теперь n -мерный вектор

d = k ₁ a ₁+ k ₂ a ₂+…+ k_n-r a _n-r - b.

Вектор d, являясь линейной комбинацией решений системы однородных уравнений (1), сам будет решением этой системы. Из (2) следует, что в решении d значения для всех свободных неизвестных равны нулю. Однако то единственное решение системы уравнений (1), которое получается при равных нулю значениях для свободных неизвестных, будет нулевым решением. Таким образом, d = 0, т. е.

b = k ₁ a ₁+ k ₂ a ₂+…+ k_n-r a _n-r.

Теорема доказана.

ð

Заметим, что приведенное доказательство позволяет утверждать, что мы получим все фундаментальные системы решений системы однородных уравнений (1), беря в качестве d всевозможные отличные от нуля определители порядка n-r.

Пример: Дана система линейных однородных уравнений

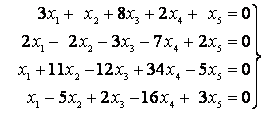
Ранг матрицы из коэффициентов равен двум, число неизвестных равно пяти, поэтому всякая фундаментальная система решений этой системы уравнений состоит из трех решений. Решим систему, ограничиваясь первыми пятью линейно независимыми уравнениями и считая x ₃, x ₄, x ₅ свободными неизвестными. Мы получим общее решение в виде

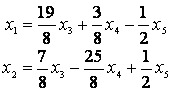
Берем, далее, следующие три линейно независимых трехмерных вектора (1, 0, 0), (0, 1, 0), (0, 0, 1). Подставляя компоненты каждого из них в общее решение в качестве значений для свободных неизвестных и вычисляя значения для x ₁ и x ₂, мы получим следующую фундаментальную систему решений заданной системы уравнений:

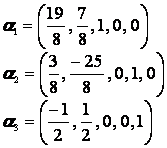
Рассмотрим, в заключении раздела связь, существующую между решениями неоднородных и однородных систем. Пусть дана система линейных неоднородных уравнений:

(3)

Система линейных однородных уравнений:

(4)

полученная из системы (3) заменой свободных членов нулями, называется приведенной системой для системы (3). Связь между решениями систем (3) и (4) определяет следующая теорема.

Теорема: Сумма и разность любого решения системы (3) с любым решением приведенной системы (4) снова будет решением системы (3).

В самом деле, пусть c ₁, c ₂,…, c _n - решение системы (3), d ₁, d ₂,…, d _n - решение системы (4). Берем любое из уравнений системы (3), например k -е, и вставляем в него вместо неизвестных числа c ₁± d ₁, c ₂± d ₂,…, c _n± d _n. Мы получим:

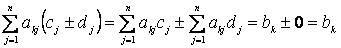
ð

Из этой теоремы вытекает, что, найдя одно решение системы линейных неоднородных уравнений (3) и складывая его с каждым из решений приведенной системы (4), получим все решения системы (3).