Сформулируем конкретную экономическую задачу и построим математическую модель, адекватную исходным данным

Задача: Механический цех выпускает три вида взаимозаменяемых деталей: А, В, С.

Каждая из деталей проходит последовательную обработку на трех станках: №1, №2, №3. Запас мощности станков составляет соответственно 220, 400 и 100 часов.

Отпускная цена деталей и время их обработки на каждом из станков приведены в таблице.

Вид детали	Время обработки детали на каждом из станков (в минутах)	Отпускная цена (в у.е.)
№1 станок	№2 станок	№3 станок
А
В
С

Требуется найти план загрузки станков, при котором выпуск продукции будет максимальным (в денежном выражении).

Построение математической модели:

Обозначим через x₁ - количество выпущенных деталей вида А;

x₂ - количество выпущенных деталей вида В;

x₃ – количество выпущенных деталей вида С.

Тогда общая стоимость выпущенной продукции составит:

f (x) = 30 x ₁ + 32 x ₂ +29 x ₃

При этом ограниченный запас мощности станков будет выражаться в модели как система линейных неравенств:

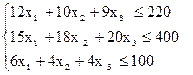
Необходимо заметить, что по смыслу задачи все переменные Х_i, где i=1,2,3, могут принимать лишь неотрицательные значения, т.е. Х_i ³ 0.

Таким образом, мы построили математическую модель интересующей нас экономической задачи:

целевая функция: f (x) = 30x₁ + 32x₂ +29x ₃ ® max

система ограничений: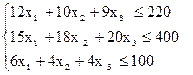

x₁ ³ 0, x₂³ 0, x₃³ 0

Построение математической модели позволяет применить для решения производственной задачи широкий спектр математических методов. Существует несколько методов решения З.Л.П. Мы рассмотрим два наиболее распространенных из них:

1. Графический метод.

2. Симплекс-метод.

Решение задачи линейного программирования

графическим методом

Графический метод решения З.Л.П. заключается в выполнении двух последовательных этапов:

I этап заключается в построении области допустимых решений. Для этого необходимо построить такой многогранник, множество всех точек которого будет совпадать с областью допустимых значений З.Л.П.

II этап предполагает вычисление оптимального решения. Для этого необходимо найти такую точку многогранника, которая будет являться оптимальным решением З.Л.П., т.е. при подстановке координат этой точки в уравнение целевой функции будет достигаться ее (функции) необходимое по смыслу задачи максимальное или минимальное значение.

Проиллюстрируем применение графического метода решения З.Л.П. на конкретном примере.

Задача: На кондитерской фабрикедля производства карамели двух видов Р₁ и Р₂ используется сахарный песок, патока и фруктовое пюре, ресурсы которых в плановый период заданы следующими числами 60 т, 80 т, 44 т соответственно. Расходы сырья на 1 т карамели соответствующего вида, а так же прибыль (у.е.) заданы в таблице:

Вид сырья	Расход сырья на 1т. карамели	Запс сырья (т)
Р1	Р2
Сахарный песок
Патока
Фруктовое пюре
Прибыль

Найти план производства карамели, при котором прибыль будет максимальной.

Построим математическую модель данной задачи:

Пусть x₁ – объем выпускаемой карамели вида Р₁ и x₂ – вида Р_2. Тогда целевая функция, отражающая объем прибыли,примет вид:

f (x) = 30x₁ + 60x₂ ® max,

а система ограничений (зависит от ресурсов сырья) будет представлена следующей системой линейных неравенств:

(1)

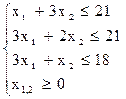
Схема выполнения I этапа. Так как целевая функция в рассматриваемой З.Л.П. содержит две переменные х₁ и х₂ , то и искомый многогранник будем строить в координатной плоскости с вумя осями координат. Одну из них обозначим через х_1, а другую через х₂.

Для того, чтобы построить многогранник, множество всех точек которого будет совпадать с областью допустимых значений З.Л.П., необходимо решить систему линейных неравенств (1). Для этого постоим на плоскости множество точек, координаты которых удовлетворяют каждому из неравенств системы.

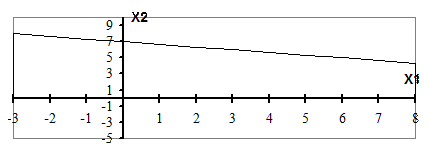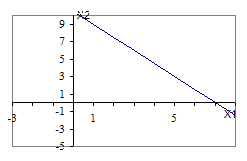
Для решения неравенства х₁ + 3х₂ £ 21 необходимо построить на плоскости прямую, заданную уравнением х₁ + 3х₂ = 21 (a). Данная прямая разбивает плоскость на две полуплоскости. Чтобы определить, какая из полуплоскостей является решением первого неравенства необходимо подставить координаты любой точки, лежащей в одной из полуплоскостей, в уравнение неравенства. Для удобства вычислений выберем точку (0;0). При подставке координат точки в уравнение неравенства получаем: 0 + 3_*0 £ 21. Это истинное неравенство.

Рисунок 1

Следовательно, решением неравенства х₁ + 3х₂ £ 21 является множество точек нижней полуплоскости, так как оно содержит точку (0;0) (рис.1).

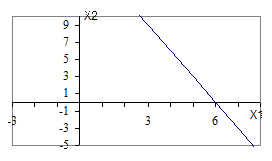Аналогично находим решение второго (3х₁ + 2х₂ £ 21) и третьего (3х₁ + х ₂ £ 18)неравенств системы ограничений (рис.2 и рис.3 соответственно).

Рисунок 2 Рисунок 3

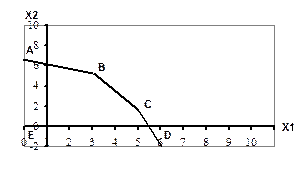Для построения многогранника допустимых решений найдем пересечение множеств решений всех неравенств (рис.4).

Рисунок 4

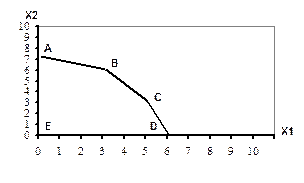Необходимо учесть, что по смыслу задачи переменные х₁ и х₂ могут принимать только неотрицательные значения. Следовательно, область допустимых решений рассматриваемой З.Л.П. будет содержать только те точки, которые расположены в первой координатной четверти (рис.5).

Рисунок 5

Таким образом, областью допустимых значений рассматриваемой З.Л.П. является замкнутый многогранник АВСДЕ.

Схема выполнения II этапа. Для нахождения точки многогранника, являющейся оптимальным решением З.Л.П. можно сравнить значение целевой функции f (x) = 30x₁ + 60x₂ во всех точках многогранника. Очевидно, что этот процесс займет бесконечный объем времени. Поэтому введем новое понятие и сократим время исследований до реальных сроков.

Определение 6 линией уровня sмы назовем множество точек плоскости, в которых целевая функция будет принимать одно и то же значение, равное s.

В нашем случае линия уровня будет задана следующим уравнением:

30x₁ + 60x₂=s

Параметр s может принимать различные значения. Вследствие чего мы получим не одну линию уровня, а семейство параллельных прямых, являющихся линиями уровня.

Замечание 1 Задача вычисления оптимального решения будет сводиться к выбору такой линии уровня, пересекающей многоранник (или касающейся его), которой соответствует наибольшее значение целевой функции (поскольку, по условию исходной задачи необходимо вычислить максимальное значение целевой функции). Замечание 2 Значение параметра s можно задатьпроизвольным образом.

Пусть s₁= 0 и s₂=240. Получили две линии уровня:

s₁: 30x₁ + 60x₂=0 иs₂: 30x₁ + 60x₂=240

Построим графики полученных линий уровня. Анализ их взаимного расположения на координатной плоскости показывает, что при перемещении линии уровня параллельно самой себе в направлении, указанном на рисунке 6 стрелкой (Þ), значение целевой функции возрастает.

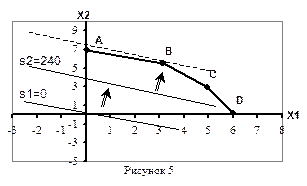Следовательно, для отыскания максимального значения целевой функции необходимо перемещать линию уровня по направлению стрелки до тех пор, пока она имеет общие точки с множеством допустимых решений.

Рисунок 6

В крайнем положении линия уровня проходит через точку В, которая лежит на пересечении прямых х₁+3х₂=21 и 3х₁+2х₂=21. Чтобы найти ее координаты необходимо решить систему линейных уравнений: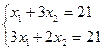

Решив систему методом подстановки получили, что х₁=3 и х₂=6. Подставим полученные значения х₁ и х₂ в уравнение целевой функции: f (x) = 30x₁ + 60x₂ = 30_*3+ 60_*6 = 450.

Таким образом, максимум целевой функции достигается в точке В (3;6) и равен 450 у.е. Сформулированная З.Л.П. решена.

Интерпретация результатов решения З.Л.П. Полученные результаты решения задачи линейного программирования имеют определенный практический смысл. В условиях сформулированной задачи можно сделать следующие выводы:

1. Максимально возможная прибыль производства карамели при существующих ресурсах в плановый период равна 450 условных единиц (так как при решении З.Л.П. было найдено, что f _max(x) = 450);

2. Для получения максимальной прибыли необходимо выпустить 3 т. карамели вида Р₁ (так как х₁=3) и 6 т. карамели вида Р₂ (так как х₂=6)_.

3. При этом ресурсы сахарного песка и патоки будут исчерпаны, так как при х₁=3 и х₂=6 первое и второе неравенства системы ограничений обращаются в тожество:

х₁+3х₂ £ 21 ® 3+3_*6=21

3х₁+2х₂ £ 21 ® 3_*3+2_*6=21;

ресурсы фруктового пюре будут сэкономлены на 3 т., так как третье неравенство системы ограничений не обращается в тождество при найденных значениях х₁ и х₂.

Действительно: 3х₁+х₂ £ 18 ® 3_*3+6 £ 18 (разность равна 3-м единицам).

Замечание 3: графический метод является наглядным способом решения З.Л.П. Но в случае большого числа переменных (более трех) графические построения становятся невозможными. Поэтому принято использовать графический метод решения З.Л.П. в основном для задач с двумя (реже - с тремя) переменными.

Замечание 4: очевидно, что в том случае, когда область допустимых решений является замкнутым контуром, оптимальное решение будет находиться либо в одной из вершин многогранника либо на одном из его ребер. Поэтому для нахождения оптимального решения З.Л.П. можно вычислить значение целевой функции в каждой из вершин многогранника допустимых решений. За оптимальное решение можно принять координаты той вершины многогранника, при которых значение целевой функции будет наибольшим.

Замечание 5: при построении области допустимых решений может получиться незамкнутый многогранник (рис.7). В этом случае З.Л.П. значение целевой функции f _max (x)=¥ (или f _min (x)=¥, в зависимости от условия задачи).

Х₂

s₂

s₁

Х₁

Рисунок 7

Решение задачи линейного программирования

симплекс – методом

Симплекс-метод является универсальным методом решения З.Л.П. Другими словами, любая задача линейного программирования может быть решена симплекс-методом.

Условимся, что данный метод мы будем применять для нахождения максимального значения целевой функции, т.е. для З.Л.П. следующего вида:

f (x) = с₁x₁+с₂x₂ +с₃x₃+…+с_nx_n ® max

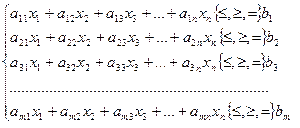
x_j ³ 0, j = 1,2,...n

где a_ij, b_i, с_j (i = 1..m; j = 1..n) – заданные постоянные величины;

x_j (j = 1..n) – неизвестные.

Замечание 6 З.Л.П. на определение минимума целевой функции необходимо заменить З.Л.П. на определение максимума целевой функции, пользуясь известным фактом: min f(x) = max(- f (x))