Рассмотрим пример решения З.Л.П. симплекс-методом по приведенному выше алгоритму

Задача: Предприятие производит продукцию двух видов Р₁ и Р₂ из сырья трех видов S₁, S₂, S₃. Запасы сырья равны соответственно b₁, b₂, b₃. Расход i -го вида сырья S_i на единицу j - го вида продукции Pj равен a_ij. Доход, получаемыйпредприятием от реализации единицы j - го вида продукции, равен с_j.

Найти план производства, обеспечивающий предприятию максимум дохода (значения всех указанных параметров приведены в таблице).

Вид сырья	Вид продукции	Ресурсы сырья bj (в у.е.)
Р1	Р2
S1	a11=4	a12=5	b1=6
S2	a21=1	а22=6	b2=8
S3	а31=1	а32=4	b3=4
Доход сj (в у.е.)

1 шаг алгоритма: пусть х₁ и х₂ - объем выпускаемой продукции вида Р₁иР₂ (соответственно). Построим математическую модель(З.Л.П.) приведенной экономической задачи:

f (x) = 7 х₁ + 5 х₂ ® max

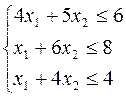
х₁³0, х₂³0

2 шаг алгоритма: сведем систему ограничений З.Л.П. к виду системы линейных уравнений. Для этого прибавим к левой части каждого неравенства дополнительные переменные. После этого сформулированная нами З.Л.П. примет вид: f (x) = 7 х₁ + 5 х₂ ® max

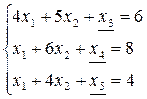
х₁³0, х₂ ³0, х₃ ³0, х₄ ³0, х₅ ³0

3 шаг алгоритма: путем элементарных преобразований необходимопривести систему ограничений к виду системы линейных уравнений с выделенными переменными. В данном случае мы уже имеем систему с выделенными переменными х₃, х₄, х₅. Так как:

- в первом уравнении системы коэффициент перед переменной х₃ равен единице, а в других уравнениях – нулю;

- во втором уравнении коэффициент перед переменной х₄ равен единице, в других уравнениях данная переменная отсутствует;

- в третьем уравнении коэффициент перед переменной х₅ равен единице, а в остальных уравнениях – нулю.

4 шаг алгоритма: найдем базисное решение, приравняв для этого небазисные переменные х₁ и х₂ к нулю, а базисные х₃, х₄, х₅ – к свободным членам: (х₁, х₂, х₃, х₄, х₅) = (0, 0, 6, 8, 4).

5 шаг алгоритма: пользуясь Теоремой 1,проверим на оптимальность полученное базисное решение.

Проведем анализ коэффициентов функции: f (x) = 7 х₁ + 5 х₂. В формуле целевой функции отсутствуют слагаемые с базисными переменными х₃, х₄, х₅, т.е. коэффициенты при них равны нулю. Коэффициенты при небазисных переменных х₁ и х₂ положительные (7>0 и 5>0 соответственно).Следовательно, найденное базисное решение (х₁, х₂, х₃, х₄, х₅) = (0, 0, 6, 8, 4) не оптимальное.

Далее по схеме 1 произведем смену одной базисной переменной. Для этого для всех коэффициентов a₁₁, a₂₁, a₃₁ (так как все они положительные!), стоящих перед переменной x₁ в системе ограничений, вычислим разрешающие коэффициенты по формуле:

r_{i =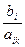} , где b_i - свободный член в i-ом уравнении.

Получим, что r₁ = 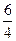= 1,5; r₂ = 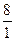= 8; r₃ = 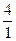= 4.

Минимальный разрешающий коэффициент r₁ = min(r₁,r₂,r₃ )=1,5. Следовательно, в 1 -ом уравнении необходимо преобразовать переменную x₁ в базисную путем эквивалентных преобразований.

1. Умножим обе части первого уравнения на действительное число λ=1/4 (чтобы коэффициент перед x₁стал равным единице).

Получили: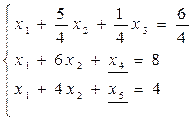

Далее, чтобы преобразовать переменную x₁ в базисную переменную, необходимо исключить ее из 2-го и 3-го уравнений. Для этого выразим в первом уравнении перемнную x₁ через небазисные переменные:

x₁ =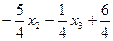

и заменим ее на полученное выражение в других уравнениях. Получим:

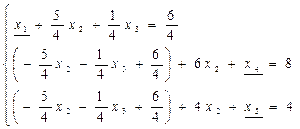
Приведем подобные члены и получим следующий вид системы ограничений:

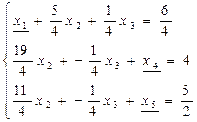
Таким образом, по определению переменная x₁будет являться базисной. Получили новое базисное решение: (х₁, х₂, х₃, х₄, х₅) = (6/4, 0, 0, 4, 5/2), где х₂, х₃ – небазисные переменные (приравниваем к нулю) и х₁, х₄, х₅ - базисные переменные (приравниваем к свободным членам).

Новое базисное решение необходимо проверить на оптимальность. При этом из целевой функции исключим новую базисную переменную x₁, выразив ее через небазисные переменные в 1 -ом уравнении.

В процессе решения мы получили, что x₁ = .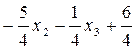

Следовательно,

f (x) =7 х₁ + 5 х₂ =7(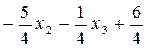) + 5 х₂ = .

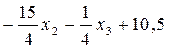Проанализируем коэффициенты перед переменными в целевой функции:

- коэффициенты перед базисными переменными х₁, х₄, х₅ равны нулю (так как отсутствуют слагаемые с этими переменными);

- коэффициенты перед не базисными переменными х₂, х₃ - отрицательные (-15/4 и –1/4 соответственно).

Следовательно, критерий оптимальности базисного решения выполнен, т.е. решение (х₁, х₂, х₃, х₄, х₅) = (6/4, 0, 0, 4, 5/2) есть оптимальное решение и max(f(x)) = .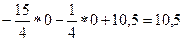

6 шаг алгоритма: интерпретируем полученные результаты.

1. План производства, обеспечивающий предприятию максимум дохода, состоит в выпуске продукции вида Р₁ объемом в 6/4 у.е. (так как х₁ = 6/4 ) и продукции вида Р₂ объемом в 0 у.е. (так как х₂ = 0).

2. Максимальная прибыль производства будет равна 10,5 условных денежных единиц (так как max(f(x))=10,5 ).

Замечание*:при увеличении числа неизвестных запись приведенного выше решения З.Л.П. становится громоздкой. Поэтому часто решение З.Л.П. симплекс - методом оформляют в виде таблицы. Такая таблица называется симплекс – таблицей.

Замечание**: при использовании симплекс-таблиц все слагаемые целевой функции, содержащие переменные, необходимо перенести в левую часть уравнения с изменением знака:

f (x) = с₁x₁+с₂x₂ +с₃x₃+…+с_nx_n ® f (x) -с₁x₁-с₂x₂ -с₃x₃-…-с_nx_n = 0.

Замечание***: изменение вида записи целевой функции сопряжено с некоторыми изменениями в условиях основных теорем (Теоремы 1, 2, 3). Учитывая данный факт, сформулируем следующие теоремы.

Теорема 1* (Критерий оптимальности неотрицательного базисного решения в задачах З.Л.П. на нахождение максимума целевой функции): Пусть в З.Л.П. с выделенными переменными все коэффициенты при небазисных переменных в целевой функции неотрицательные, а при базисных равны нулю. Тогда базисное решение, соответствующее данному виду З.Л.П., является оптимальным.

Теорема 2* (Критерий неограниченности значений целевой функции): Пусть в З.Л.П. (на максимум) с выделенными переменными некоторый коэффициент в целевой функции с _к < 0 при переменной х_к, и пусть в системе ограничений перед переменной х_к все коэффициенты а^’_iк £ 0. Тогда значения целевой функции не ограничены на максимум (f _max (x) = ¥).

Теорема 3 (О возможности перехода от одного базисного решения к другому с не меньшим значением целевой функции): Пусть в З.Л.П. (на максимум) с выделенными переменными в целевой функции некоторый коэффициент с _к < 0 при переменной х_к, и в системе ограничений среди коэффициентов перед этой переменной есть положительные (а^’_iк >0). Тогда можно перейти от данного базисного решения к другому, с не меньшим значением целевой функции.