1 шаг: привести целевую функцию f (x) = с1x1+с2x2 +с3x3+…+сnxn к виду: f (x) -с1x1-с2x2 -с3x3-…-сnxn = 0.
2 шаг: свести систему ограничений к системе линейных уравнений путем добавления дополнительных переменных.
3 шаг: путем эквивалентных преобразований представить систему ограничений в виде системы линейных уравнений с выделенными переменными.
4 шаг: заполнить симплекс-таблицу (предположим, что первые m переменные – базисные):
| Базис | Свободные члены | Переменные | Разрешающий коэффициент | ||||
| x1 | x2 | x3 | … | xn | |||
| x1 | b1 | a11 | a12 | a13 | … | a1n | ri = 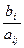 , для aij > 0 , для aij > 0 |
| x2 | b2 | a21 | a22 | a23 | … | a2n | |
| … | … | … | … | … | … | … | |
| xm | bm | am1 | am2 | am3 | … | amn | |
| f (x) | 0 | с1 | с2 | с3 | … | сn |
5 шаг: пользуясь Теоремой 1*,проверить базисное решение на оптимальность:
Þесли все коэффициенты целевой функции при небазисных переменных положительные,а при базисных равны нулю, то критерий оптимальности выполнен. Далее перейти к 6-му шагу алгоритма.
Þесли в целевой функции найдется хотя бы один отрицательный коэффициент сj перед небазисной переменной xj, тонайденное базисное решение не является оптимальным. В этом случае, пользуясь теоремой 3*,исследуют возможность перехода к новому базисному решению. Если получили, что такой переход возможен, то необходимо осуществить смену одной базисной переменной по схеме 1*.
Схема 1*
- Пусть в целевой функции при небазисной переменной xj коэффициент сj < 0. Тогда для всех положительных коэффициентов aik, стоящих в столбце “xj” симлекс-таблицы, вычисляют разрешающий коэффициент по формуле:
ri = 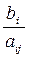 , где bi - свободный член в i-ой строке таблицы.
, где bi - свободный член в i-ой строке таблицы.
- Среди всех разрешающих коэффициентов находят минимальный. Пусть rp = min (ri ). Тогда в p -ой строке таблицы производят замену исходной базисной переменной на переменную xj.
- После смены одной базисной переменной необходимо путем эквивалентных преобразований привести симплекс-таблицу к следующему виду:
| Базис | Свободные члены | Переменные | Разрешающий коэффициент | ||||||
| x1 | x2 | x3 | … | xj | … | xn | |||
| x1 | b1’ | a11’ | a12’ | a13’ | … | … | a1n’ | ri = 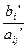 , для aij’ > 0 , для aij’ > 0 | |
| x2 | b2’ | a21’ | a22’ | a23’ | … | … | a2n’ | ||
| … | … | … | … | … | … | … | … | ||
| xp xj | 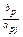 | 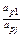 | 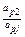 | 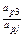 | … | … | 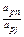 | ||
| … | … | … | … | … | … | … | … | ||
| xm | bm’ | am1’ | am2’ | am3’ | … | … | amn’ | ||
| f (x) | c | с1’ | с2’ | с3’ | … | … | сn’ |
-Теперь переменная xj будет являться базисной. Получили новое базисное решение. Его необходимо проверить на оптимальность по теореме 1*. Если найденное базисное решение является оптимальным, то перейти к 6 шагу алгоритма. В противном случае необходимо произвести смену одной базисной переменной по схеме 1*.
6 шаг: сформулировать выводы по результатам решения З.Л.П.
Проиллюстрируем использование симплекс-таблицы для решения З.Л.П. следующего вида:
f (x) = х1 + х2 – х3 ® max
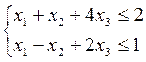
х1 ³0, х2 ³0, х3 ³0
1 шаг алгоритма: приведем целевую функцию f (x) = х1+ х2 – х3
к виду: f (x) - х1 - х2 + х3 = 0.
2 шаг алгоритма: сведем систему ограничений к системе линейных уравнений путем добавления дополнительных переменных х4 и х5:
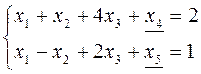
х1 ³0, х2 ³0, х3 ³0, х4 ³0, х5 ³0
3 шаг алгоритма: в данном случае, после ввода дополнительных переменных,в каждой из двух уравнений системы уже присутствует выделенная переменная (х4 - в первом уравнении и х5 – во втором).
4 шаг алгоритма: заполним симплекс-таблицу (Табл.1):
Таблица 1
| Базис | Свободные члены | Переменные | Разрешающий коэффициент | ||||
| х1 | х2 | х3 | х4 | х5 | |||
| х4 | 2/1=2 | ||||||
| х5 | -1 | 1/1=1min | |||||
| f(x) | -1 | -1 |
Базисное решение имеет вид: (х1,х2,х3,х4,х5)=(0,0,0,2,1). Найденное базисное решение не является оптимальным, так как не все коэффициенты целевой функции неотрицательные. Следовательно, необходимо осуществить смену одной базисной переменной. Для этого выберем одну из переменных, при которой в целевой функции стоит отрицательный коэффициент (например, переменную х1) и произведем для этой переменной расчет разрешающих коэффициентов (Табл. 1).
Поскольку наименьший из разрешающих коэффициентов стоит во второй строке таблицы, то необходимо заменить базисную переменную х5 на переменную х1. Так как теперь х1 является базисной переменной, то необходимо путем эквивалентных преобразований получить а11=0, с1=0 и а21=1.
В данном случае, чтобы получить:
а 21 =1, необходимо разделить вторую строку таблицы на разрешающий коэффициент;
а 11 =0, необходимо вычесть из элементов первой строки соответствующие элементы второй;
с 1 =0, необходимо сложить вторую и третью строку таблицы.
После указанных преобразований получим таблицу 2 (стр.28).
Получили новое базисное решение (х1,х2,х3,х4,х5)=(1,0,0,1,0). Выделенное базисное решение не доставляет максимума целевой функции (не является оптимальным), так как не все коэффициенты целевой функции являются неотрицательными числами.
Таблица 2
| Базис | Свободные члены | Переменные | ||||
| х1 | х2 | х3 | х4 | х5 | ||
| х4 | -1 | |||||
| х1 | -1 | |||||
| f(x) | -2 |
Так перед переменной х2 в целевой функции стоит коэффициент с2 = -2. Следовательно, необходимо произвести смену одной базисной переменной. Но, поскольку в столбце «х2» (Табл. 2) присутствует только один положительный коэффициент а12 = 2, стоящий в первой стоке таблицы, то нет необходимости в расчете разрешающих коэффициентов. Можно сразу сделать вывод, что базисную переменную х4 необходимо заменить напеременную х2. Так как теперь х2 является базисной переменной, то необходимо путем эквивалентных преобразований получить а12=1, с2=0 и а22=0.
В данном случае, чтобы получить:
с 1 =0, необходимо сложить вторую и третью строку таблицы;
а 12 =1, необходимо разделить вторую строку таблицы на 2;
а 22 =0, необходимо прибавить к элементам второй строки соответствующие элементы первой, полученные после умножения на 2;
Внесем все преобразования в таблицу 3.
Таблица 3
| Базис | Свободные члены | Переменные | Разрешающий коэффициент | ||||
| х1 | х2 | х3 | х4 | х5 | |||
| х2 | 1/2 | 1/2 | -1/2 | ||||
| х1 | 3/2 | 1/2 | 1/2 | ||||
| f(x) |
По таблице 3 составим новое базисное решение, приравнивая базисные переменные к свободным членам, небазисные – к нулю: (х1,х2,х3,х4,х5) = (3/2, 1/2,0,0,0). Данное базисное решение является оптимальным (по теореме 1*), так как все коэффициенты целевой функции есть неотрицательные числа. Следовательно, найденный базис будет доставлять максимальное значение целевой функции: f (x) = х1 + х2 – х3 . Таким образом, max (f (x)) = 2 + 5х3 + х4 = 2. Поставленная З.Л.П решена.
 Задачи для самостоятельного решения
Задачи для самостоятельного решения
Задание 1. Решить графическим методом задачу линейного программирования. Найти максимум и минимум функции F(x) при заданных ограничениях.
1. F(x)=10х1 +5х2 2. F(x)=3х1 +5х2 3. F(x)=4х1- 3х2
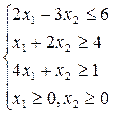
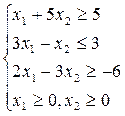
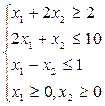
4. F(x)=5х1+ 10х2 5. F(x)=2х1+ х2 6. F(x)=3х1+3 х2
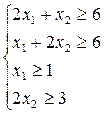
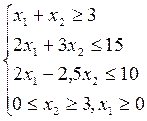
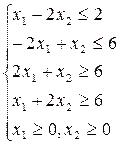
Задание 2. Предприятие производит продукцию 2-х видов Р1 и Р2 из сырья 3-х видов а1, а2, а3. Запасы сырья равны соответственно b1, b2, b3. Расход i-го вида сырья (аi) на единицу j-го вида продукции (Рj) равен аij.
Найти план производства, обеспечивающий предприятию максимум дохода (значения всех параметров приведены в таблице 1-9).
Решить задачу графическим способом.
Таблица 1. Таблица 2. Таблица 3.
| Р1 | Р2 | bi | Р1 | Р2 | bi | Р1 | Р2 | bi | |||||
| а1 | а1 | а1 | |||||||||||
| а2 | а2 | а2 | |||||||||||
| а3 | а3 | а3 | |||||||||||
| сi | сi | сi |
Таблица 4. Таблица 5. Таблица 6.
| Р1 | Р2 | bi | Р1 | Р2 | bi | Р1 | Р2 | bi | |||||
| а1 | а1 | а1 | |||||||||||
| а2 | а2 | а2 | |||||||||||
| а3 | а3 | а3 | |||||||||||
| сi | сi | сi |
Таблица 7(Горяев). Таблица 8(Максимова). Таблица 9(Фатеева).
| Р1 | Р2 | bi | Р1 | Р2 | bi | Р1 | Р2 | bi | |||||
| а1 | а1 | а1 | |||||||||||
| а2 | а2 | а2 | |||||||||||
| а3 | а3 | а3 | |||||||||||
| сi | сi | сi |
Задание 3. Решить задачу линейного программирования симплекс – методом.
1. Найти максимум функции: 2. Найти максимум функции:
F(x)=х1 +х2 F(x)=-6х1 -4х2+4 х3
при ограничениях: при ограничениях:
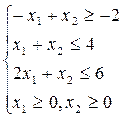
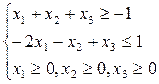
3. Найти максимум функции: 4. (Горяев)Найти минимум функции:
F(x)=6х1-2х2+4х3 F(x)= -6х1 +4х2+4 х3
при ограничениях: при ограничениях:
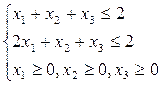
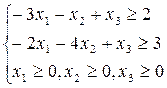
5. (Максимова)Найти минимум функции: 6. (Фатеева)Найти максимум функции:
F(x)=2х1+4х2+6х3 F(x)= 3х1 +х2
при ограничениях: при ограничениях:
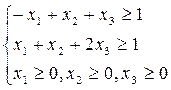
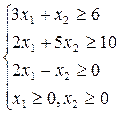
Задание 4. Для изготовления трех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и прибыль от реализации каждого продукта приведены в таблице 10 -12.
Найти план производства, при котором достигается максимальная прибыль. Решить задачу симплекс-методом.
Таблица 10.
| Тип сырья | Нормы расхода сырья на одно изделие | Запасы сырья | ||
| А | Б | В | ||
| Цена изделия |
Таблица 11.
| Тип сырья | Нормы расхода сырья на одно изделие | Запасы сырья | ||
| А | Б | В | ||
| Цена изделия |
Таблица 12.
| Тип сырья | Нормы расхода сырья на одно изделие | Запасы сырья | ||
| А | Б | В | ||
| Цена изделия |
Задание 5. Для изготовления четырех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и прибыль от реализации каждого продукта приведены в таблице 13 -15.
Найти план производства, при котором достигается максимальная прибыль.
Решить задачу симплекс-методом (использовать симплекс-таблицу).
Таблица 13.
| Тип сырья | Нормы расхода сырья на одно изделие | Запасы сырья | |||
| А | Б | В | Г | ||
| Цена изделия |
Таблица 14.
| Тип сырья | Нормы расхода сырья на одно изделие | Запасы сырья | |||
| А | Б | В | Г | ||
| Цена изделия |
Таблица 15.
| Тип сырья | Нормы расхода сырья на одно изделие | Запасы сырья | |||
| А | Б | В | Г | ||
| Цена изделия |
Задание 6. Механический цех выпускает три вида взаимозаменяемых деталей: А, В, С.
Каждая из деталей проходит последовательную обработку на трех станках: №1, №2, №3. Запас мощности станков составляет соответственно 220, 400 и 100 часов.
Отпускная цена деталей и время их обработки на каждом из станков приведены в таблице 16.
Таблица 16.
| Вид детали | Время обработки детали на каждом из станков (в минутах) | Отпускная цена (в у.е.) | ||
| №1 станок | №2 станок | №3 станок | ||
| А | ||||
| В | ||||
| С |
Требуется найти план загрузки станков, при котором выпуск продукции будет максимальным (в денежном выражении).
дополнительная литература
1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах.-М.:Высшая школа, 1999, 1ч.
2. Кондаков В.М. Математическое программирование. Элементы линейной алгебры и линейного программирования. Уч. пособие.-Пермь, 1997.
3. Ларионов А.И., Юрченко Т.И., Новоселов А.Л. Экономико-математические методы в планировании.-М.:Высшая школа, 1991.
4. Ромахин М.И. Элементы линейной алгебры и линейного программирования.-М.:Высшая школа, 1963.
5. Карасев А.И., Кремер Н.Ш., Савельева Т.И. Математические методы и модели в планировании. -М.:Экономика,1987.
6. Канторович Л.В., Горстко А.Б. Оптимальные решения в экономике.-М.:Наука,1972.
 2015-06-10
2015-06-10 1614
1614
