Л.В. Канторович совместно с М. К. Гавуриным разработали в 1949 г. Метод потенциалов, который применяется при решении транспортных задач. В последующих работах Л.В. Канторовича, В. С. Немчинова, В. В. Новожилова, и других математиков и экономистов получили дальнейшее развитие как математическая теория линейного программирования, так и приложение её методов к исследованию различных экономических проблем.
Пусть однородный груз сосредоточен у m поставщиков в объемах a1,a2,…,am. Имеющийся груз необходимо доставить n потребителям в объемах b1,b2,…,bn. Известна стоимость cij, перевозки единицы груза из i- го пункта отправления (i=1,2,…,m), в j -й пункт назначения (j=1,2,…,n). Требуется составить такой план перевозок, при котором запасы всех поставщиков будут вывезены полностью, запросы всех потребителей - удовлетворены и суммарные транспортные издержки минимальны.
Для построения экономико-математической модели рассмотрим матрицу
Х = 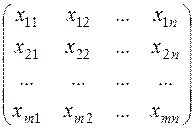 ,
,
где xij – количество единиц груза, которое необходимо доставить из i- го пункта отправления, в j- й пункт назначения, i=1,2,…,m, j=1,2,…,n. Матрицу Х будем называть матрицей перевозок, или планом. Предполагается, что 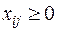 . Удельные транспортные расходы запишем в виде матрицы
. Удельные транспортные расходы запишем в виде матрицы
С = 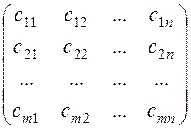 ,
,
и назовем ее матрицей тарифов.
Исходные данные транспортной задачи обычно записываются в таблице (таблица 3.1), которую будем называть распределительной.
Таблица 3.1
| bj | b1 | b2 | … | bn |
| ai | ||||
| a1 | c11 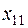 | c12 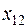 | … | 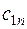 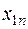 |
| a2 | 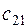 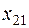 | c22 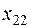 | … | c2n 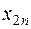 |
| … | … | … | … | … |
| am | cm1 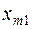 | cm2 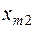 | … | cmn 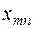 |
Так как произведение 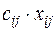 определяет затраты на перевозку груза от i –го поставщика j –му потребителю, то суммарные затраты на перевозку всех грузов равны
определяет затраты на перевозку груза от i –го поставщика j –му потребителю, то суммарные затраты на перевозку всех грузов равны 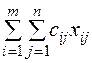 . По условию задачи требуется обеспечить минимум суммарных затрат. Следовательно, целевая функция имеет вид
. По условию задачи требуется обеспечить минимум суммарных затрат. Следовательно, целевая функция имеет вид
Z(X) = 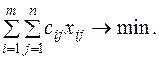
Система ограничений задачи состоит из двух групп уравнений. Первая группа из m уравнений описывает тот факт, что запасы всех m поставщиков вывозятся полностью:
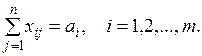
Вторая группа из n уравнений выражает требование полностью удовлетворить запросы всех n потребителей:
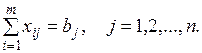
Учитывая условие не отрицательности объемов перевозок, математическую модель задачи можно записать так:
Z(X) = 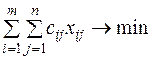 , (3.1)
, (3.1)
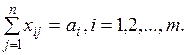 (3.2)
(3.2)
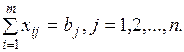 (3.3)
(3.3)
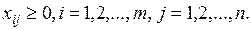 (3.4)
(3.4)
Если в модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей, т.е.
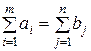 (3,5)
(3,5)
то такая модель называется закрытой. Если же это равенство не выполняется, то такая модель называется открытой.
Теорема 3.1. Для того чтобы транспортная задача линейного программирования имела решение, необходимо и достаточно, чтобы суммарные запасы поставщиков равнялись суммарным запасам потребителей
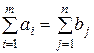 , т.е. модель задачи должна быть закрытой.
, т.е. модель задачи должна быть закрытой.
Открытую модель ТЗ можно свести к закрытой. Пусть суммарные запасы поставщиков превосходят суммарные запросы потребителей, т.е. 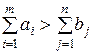 .
.
Очевидно, что в этом случае при составлении оптимального плана перевозок часть запасов поставщиков, равная 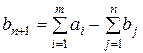 останется не вывезенной. В этом случае необходимо ввести фиктивного потребителя с запросами
останется не вывезенной. В этом случае необходимо ввести фиктивного потребителя с запросами 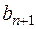 равными разности суммарных запасов поставщиков и запросов потребителей, и нулевыми стоимостями перевозок единиц груза
равными разности суммарных запасов поставщиков и запросов потребителей, и нулевыми стоимостями перевозок единиц груза 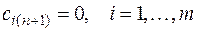 . Аналогично в случае, когда суммарные запросы потребителей превосходят суммарные запасы поставщиков, т.е.
. Аналогично в случае, когда суммарные запросы потребителей превосходят суммарные запасы поставщиков, т.е. 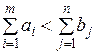
часть запросов потребителей, равная 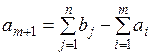
останется не удовлетворенной. Для того чтобы задача в рассматриваемом случае имела решение, необходимо ввести фиктивного поставщика с запасами 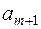 равными разности суммарных запасов поставщиков и запросов потребителей, и нулевыми стоимостями перевозок единиц груза
равными разности суммарных запасов поставщиков и запросов потребителей, и нулевыми стоимостями перевозок единиц груза 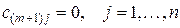 .
.
Пример 1. Рассмотрим транспортную задачу, исходные данные которой приведены в табл. 3.2
Таблица 3.2
Проверяем выполнение необходимого и достаточного условия разрешимости задачи. Находим суммарные запасы поставщиков и запросы потребителей:
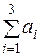 = 100 + 200 + 300 = 600,
= 100 + 200 + 300 = 600, 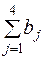 = 100 + 100 + 300 + 300 = 800.
= 100 + 100 + 300 + 300 = 800.
Задача открытая. Вводим четвертого, фиктивного поставщика с запасами а4 = 800 — 600 = 200 и нулевыми стоимостями перевозки единиц груза (табл. 3.3)
Таблица 3.3
| bj | |||||||||
Система ограничений ТЗ (3.2), (3.3) представляет собой линейную алгебраическую систему вида 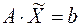 . (3.6)
. (3.6)
Здесь вектор 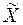 размерности
размерности 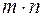 и имеет координаты
и имеет координаты 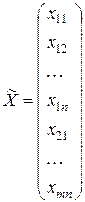 .
.
Теорема 3.2. Ранг матрицы A транспортной задачи (ТЗ) на единицу меньше числа уравнений 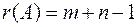 .
.
Клетки таблицы транспортной задачи, в которых находятся отличные от нуля или базисные нулевые перевозки, называются занятыми, остальные — незанятыми или свободными.
Циклом назовем такую последовательность занятых клеток распределительной таблицы ТЗ, в которой две и только две соседние клетки расположены в одной строке или столбце, причем первая и последняя клетки также находятся в одной строке или столбце.
Цикл изображают в таблице ТЗ в виде замкнутой, ломаной линии. В любой клетке цикла происходит поворот звена ломаной линии на 90°. Простейшие циклы изображены на рис. 2, где звездочкой отмечены клетки таблицы, включенные в состав цикла.

Рис 2.
Допустимым решением ТЗ будем называть такую матрицу X, компоненты которой удовлетворяет системе (3.2), (3.3).
Опорным решением ТЗ будем называть любое допустимое решение, которое имеет отличных от нуля координат не более m + n -1, причем из занятых клеток не образуются циклы.
Число отличных от нуля координат невырожденного опорного решения равно m + n - 1, а для вырожденного опорного решения меньше m + n -1.
Начальное опорное решение построим методом минимального элемента. Метод минимальной стоимости прост, он позволяет построить опорное решение, достаточно близкое к оптимальному, так как использует матрицу стоимостей транспортной задачи С = 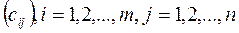 . Он состоит из ряда однотипных шагов, на каждом из которых заполняется только одна клетка таблицы, соответствующая минимальной стоимости
. Он состоит из ряда однотипных шагов, на каждом из которых заполняется только одна клетка таблицы, соответствующая минимальной стоимости 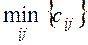
 , и исключается из рассмотрения только одна строка (поставщик) или один столбец (потребитель). Очередную клетку, соответствующую
, и исключается из рассмотрения только одна строка (поставщик) или один столбец (потребитель). Очередную клетку, соответствующую 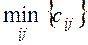 заполняют по следующим правилам. Поставщик исключается из рассмотрения, если его запасы использованы полностью. Потребитель исключается из рассмотрения, если его запросы удовлетворены полностью. На каждом шаге исключается либо один поставщик, либо один потребитель. При этом если поставщик еще не исключен, но его запасы равны нулю, то на том шаге, когда от данного поставщика требуется поставить груз, в соответствующую клетку таблицы заносится базисный нуль, и лишь затем поставщик исключается из рассмотрения. Аналогично с потребителем.
заполняют по следующим правилам. Поставщик исключается из рассмотрения, если его запасы использованы полностью. Потребитель исключается из рассмотрения, если его запросы удовлетворены полностью. На каждом шаге исключается либо один поставщик, либо один потребитель. При этом если поставщик еще не исключен, но его запасы равны нулю, то на том шаге, когда от данного поставщика требуется поставить груз, в соответствующую клетку таблицы заносится базисный нуль, и лишь затем поставщик исключается из рассмотрения. Аналогично с потребителем.
Теорема 3.3. Решение транспортной задачи, построенное методом минимальной стоимости, является опорным.
Пример 2. Используя метод минимальной стоимости, построить начальное опорное решение транспортной задачи, исходные данные которой приведены в табл. 3.4.
Таблица 3.4
| ai | bj | ||||||||
Среди элементов матрицы стоимостей выбираем наименьшую стоимость с11=1, отмечаем ее кружочком. Это стоимость перевозки груза от 1-го поставщика 1-му потребителю. В соответствующую клетку (1, 1) записываем максимально возможный объем перевозки х11 = min {a1 b1} = min {60, 40} = 40 (табл. 3.5). Запасы 1-го поставщика уменьшаем на 40, т.е. 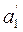 = а1 — b1 = 60 — 40 = 20.
= а1 — b1 = 60 — 40 = 20.
Исключаем из рассмотрения 1-го потребителя, так как его запросы удовлетворены и вычеркиваем 1-й столбец.
Теперь минимальной является стоимость с14 = 2. Максимально возможная перевозка, которую можно осуществить от 1-го поставщика 4-му потребителю, равна х14= min{ 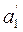 , b4} = min{20, 60} = 20. В соответствующую клетку таблицы записываем перевозку х14 = 20. Запасы 1-го поставщика исчерпаны, исключаем его из рассмотрения, вычеркивая первую строку.
, b4} = min{20, 60} = 20. В соответствующую клетку таблицы записываем перевозку х14 = 20. Запасы 1-го поставщика исчерпаны, исключаем его из рассмотрения, вычеркивая первую строку.
Таблица 3.5
 bj ai bj ai | |||||||||
Запросы 4-го потребителя уменьшаем на 20, т.е.
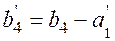 = 60 - 20 = 40.
= 60 - 20 = 40.
В оставшейся части распределительной таблицы минимальная стоимость с24 = с32 = 3. Заполняем одну из двух клеток таблицы (2, 4) или (3, 2). Пусть в клетку (2, 4) записываем х24 = min {а2, b4} = min {80, 40} = 40. Запросы 4-го потребителя удовлетворены, исключаем его из рассмотрения, вычеркиваем четвертый столбец. Уменьшаем запасы 2-го поставщика 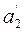 = а2 — b4 = 80 — 40 = 40.
= а2 — b4 = 80 — 40 = 40.
Теперь минимальная стоимость min {сij} = с32 = 3. Записываем в клетку таблицы (3, 2) перевозку x32 = min {а3, b2} = min {100, 60} = 60. Исключаем из рассмотрения 2-го потребителя, а из распределительной таблицы - второй столбец и вычисляем 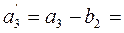 100 — 60 = 40.
100 — 60 = 40.
Определяем минимальную стоимость min {сij} = = с33 = 6 и записываем в клетку таблицы (3, 3) перевозку х33 = min { 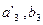 } = = min {40, 80} = 40. Исключаем из рассмотрения 3-го поставщика и третью строку распределительной таблицы. Определяем
} = = min {40, 80} = 40. Исключаем из рассмотрения 3-го поставщика и третью строку распределительной таблицы. Определяем
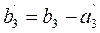 = 80 - 40 = 40.
= 80 - 40 = 40.
Остается единственный элемент с23 = 8. Записываем в клетку таблицы (2, 3) перевозку х23 = 40.
Число занятых клеток таблицы равно N = m + n - 1 = 3 + 4- 1 = 6, следовательно решение является опорным.
Широко распространенным методом решения транспортных задач является метод потенциалов.
Теорема 3.4 (признак оптимальности опорного решения). Если допустимое решение ТЗ Х= 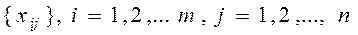
является оптимальным, то ему соответствует система из 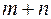 чисел
чисел 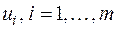 и потребителей
и потребителей 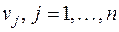 удовлетворяющие следующим условиям:
удовлетворяющие следующим условиям: 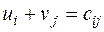 , при xij > 0, (3.7)
, при xij > 0, (3.7)
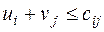 , при xi j = 0 (3.8)
, при xi j = 0 (3.8)
Числа 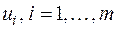 и
и 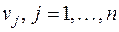 называются потенциалами соответственно i – го поставщика и j – гопотребителя.
называются потенциалами соответственно i – го поставщика и j – гопотребителя.
Группа равенств (3.7) ui + vj =cij при xij > 0 используется как система уравнений для нахождения потенциалов. Так как число неизвестных системы на единицу больше числа уравнений, то одной из них можно задать значение произвольно, а остальные найти из системы уравнений.
Группа неравенств (3.8) 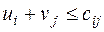 , при xi j = 0 используется для проверки оптимальности опорного решения. Эти неравенства удобно записать в виде
, при xi j = 0 используется для проверки оптимальности опорного решения. Эти неравенства удобно записать в виде 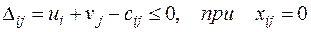 . (3.9)
. (3.9)
Числа Δij называются оценками свободных клеток таблицы.
Пример 3. Рассмотрим задачу из примера 1. Методом минимального элемента построим начальное опорное решение
Таблица 3.6
| bj | |||||||||
| 200* |
Полученное решение 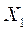 имеет m + n - 1=4 + 4— 1 = 7 занятых клеток. Опорное решение является вырожденным, так как одна из его координат равна нулю. Вычислим значение целевой функции на этом опорном решении
имеет m + n - 1=4 + 4— 1 = 7 занятых клеток. Опорное решение является вырожденным, так как одна из его координат равна нулю. Вычислим значение целевой функции на этом опорном решении
f(X1) = 100 • 1 + 0 • 2 + 100 • 3 + 100 • 4 + + 200 • 7 + 100 • 12 + 200•0 = 3400.
Для проверки оптимальности опорного решения необходимо найти потенциалы. По признаку оптимальности в каждой занятой опорным решением клетке таблицы транспортной задачи сумма потенциалов равна стоимости 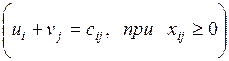 .
.
Записываем систему уравнений для нахождения потенциалов:
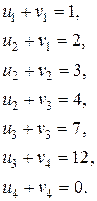
Система состоит из семи уравнений и имеет восемь переменных. Система неопределенная. Одному из потенциалов задаем значение произвольно: пусть 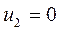 . Остальные потенциалы находятся однозначно:
. Остальные потенциалы находятся однозначно:

Значения потенциалов записываем рядом с запасами или запросами соответствующих поставщиков и потребителей в таблицу (табл. 3.7). Система уравнений для нахождения потенциалов достаточно проста, обычно ее решают устно, глядя на таблицу задачи, ее занятые клетки и известные потенциалы.
Таблица 3.7
  1 - 100 1 - 100 |  1 + 1 + | 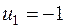 | |||
 2 + 0 2 + 0 | 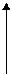 4 - 100 4 - 100 | 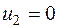 | |||
 7 + 200 7 + 200 | - 100 | 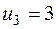 | |||
| 200* | 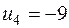 | ||||
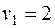 | 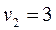 | 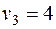 | 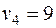 |
Проверяем опорное решение 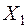 на оптимальность. С этой целью вычисляем оценки
на оптимальность. С этой целью вычисляем оценки 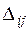 для всех незаполненных клеток таблицы (для всех занятых клеток
для всех незаполненных клеток таблицы (для всех занятых клеток 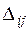 = 0);
= 0);
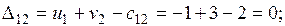
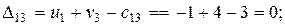
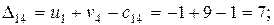
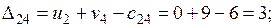
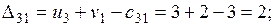
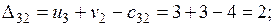
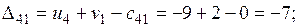
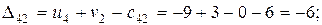
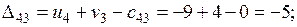
Решение не оптимально.
Оценки для свободных клеток транспортной таблицы используются для улучшения опорного решения. С этой целью находят клетку (l, к) таблицы, соответствующую 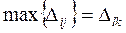 . Если
. Если 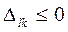 , то решение оптимальное. Если же
, то решение оптимальное. Если же 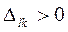 , то для соответствующей клетки (l, к) строят цикл и улучшают решение, перераспределяя груз
, то для соответствующей клетки (l, к) строят цикл и улучшают решение, перераспределяя груз 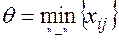 по этому циклу.
по этому циклу.
Пример 4. Переходим к новому опорному решению. Находим клетку таблицы, которой соответствует наибольшая положительная оценка:
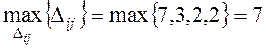
это у клетки (1,4). Для этой клетки строим цикл. Ставим в нее знак «+», присоединяем ее к занятым клеткам и применяем метод вычеркивания. После проведения вычеркиваний в таблице остаются только образующие цикл клетки. Цикл изображен в табл.3.7. На основании одной из теорем ТЗ такой цикл единственный. В угловых точках цикла расставляем поочередно знаки «+» и «-», начиная с «+» в клетке (1, 4). В клетки, отмеченные знаком «+», прибавляется груз 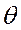 , а из клеток, отмеченных знаком «-», вычитается такой же по величине груз. Определяем величину груза
, а из клеток, отмеченных знаком «-», вычитается такой же по величине груз. Определяем величину груза 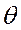 , перераспределяемого по циклу. Она равна значению наименьшей из перевозок в клетках цикла, отмеченных знаком «-»,
, перераспределяемого по циклу. Она равна значению наименьшей из перевозок в клетках цикла, отмеченных знаком «-»,
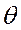 = min{100, 100, 100} = 100. Осуществляем сдвиг по циклу на величину
= min{100, 100, 100} = 100. Осуществляем сдвиг по циклу на величину 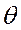 . Получаем второе опорное решение
. Получаем второе опорное решение 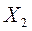 (табл. 3.8).
(табл. 3.8).
Таблица 3.8
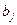 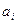 | ||||||||
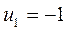  | ||||||||
 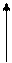 -3 -3 | 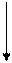 + 4 + 4 | 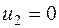 | ||||||
+ | - | 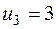 | ||||||
| 200* | 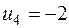 | |||||||
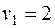 | 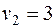 | 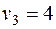 | 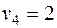 |
В данном случае минимум перевозок в клетках, отмеченных знаком «-», достигался сразу в трех клетках, поэтому для того, чтобы число занятых клеток опорного решения было по-прежнему равно m + n - 1 = 7, в клетки с номерами (1, 1) и (2, 3) поставлены нулевые базисные перевозки. Следует освобождать клетку с большей стоимостью перевозки, т.е. клетку (3, 4).
Вычисляем значение целевой функции на втором опорном решении:
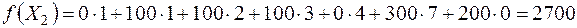 .
.
Проверяем второе опорное решение 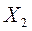 на оптимальность. Находим потенциалы и оценки. Они приведены в табл. 3.8. Решение не является оптимальным, так как имеются положительные оценки
на оптимальность. Находим потенциалы и оценки. Они приведены в табл. 3.8. Решение не является оптимальным, так как имеются положительные оценки 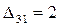 ,
, 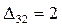 ,
, 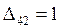 , и
, и 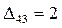 . Наибольшая из них равна 2 одновременно для трех клеток (3, 1), (3, 2) и (4, 3). В одну из них, пусть в клетку (3, 2), ставим знак «+». Для этой клетки строим цикл (см. табл. 3.8) и находим величину груза для перераспределения по циклу:
. Наибольшая из них равна 2 одновременно для трех клеток (3, 1), (3, 2) и (4, 3). В одну из них, пусть в клетку (3, 2), ставим знак «+». Для этой клетки строим цикл (см. табл. 3.8) и находим величину груза для перераспределения по циклу: 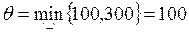 . Осуществляем сдвиг по циклу на величину
. Осуществляем сдвиг по циклу на величину 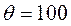 . Получаем третье опорное решение (табл. 3.9).
. Получаем третье опорное решение (табл. 3.9).
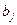 | ||||||||
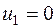 | ||||||||
 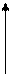 2 100 - 2 100 - | + 4
| 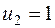 | ||||||
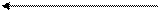 + + | 200 - | 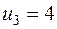 | ||||||
| 200* | 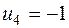 | |||||||
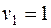 | 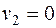 | 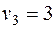 | 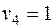 |
Вычисляем значение целевой функции на третьем опорном решении:
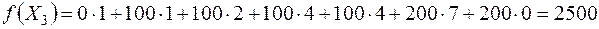 .
.
Проверяем третье опорное решение на оптимальность. Находим потенциалы и оценки. Они приведены в табл. 3.9. Решение не является оптимальным, так как имеются положительные оценки 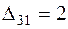 и
и 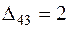 . В одну из клеток с положительной оценкой, пусть в клетку (3, 1), ставим знак «+». Для этой клетки строим цикл (см. табл. 3.9) и находим величину груза для перераспределения по циклу:
. В одну из клеток с положительной оценкой, пусть в клетку (3, 1), ставим знак «+». Для этой клетки строим цикл (см. табл. 3.9) и находим величину груза для перераспределения по циклу: 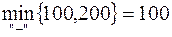 . Осуществляем сдвиг по циклу на величину
. Осуществляем сдвиг по циклу на величину 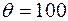 . Получаем четвертое опорное решение
. Получаем четвертое опорное решение 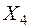 (табл. 3.10).
(табл. 3.10).
Таблица 3.10
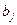 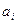 | |||||
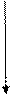  1 0 - 1 0 - |  1 100 + 1 100 + | 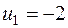 | |||
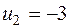 | |||||
 3 100 + 3 100 + |  7 100 - 7 100 - | 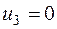 | |||
| 200* |  + + | 200 - | 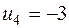 | ||
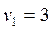 | 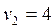 | 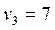 | 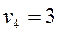 |
Вычисляем значение целевой функции на четвертом опорном решении:
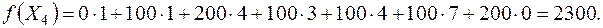
Проверяем решение 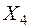 на оптимальность. Находим потенциалы и оценки. Они приведены в табл. 3.10. Положительными являются оценки
на оптимальность. Находим потенциалы и оценки. Они приведены в табл. 3.10. Положительными являются оценки 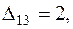
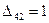 и
и 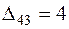 . Для клетки (4, 3), которой соответствует наибольшая оценка, строим цикл (см. табл.3.10) и находим величину груза для перераспределения по циклу:
. Для клетки (4, 3), которой соответствует наибольшая оценка, строим цикл (см. табл.3.10) и находим величину груза для перераспределения по циклу: 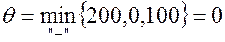 . Осуществляем сдвиг по циклу на величину
. Осуществляем сдвиг по циклу на величину 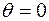 . Получаем пятое опорное решение
. Получаем пятое опорное решение 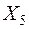 (табл. 3.11):
(табл. 3.11):
Таблица 3.11
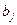 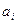 | |||||
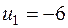 | |||||
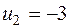 | |||||
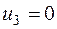 | |||||
| 200* | 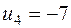 | ||||
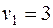 | 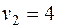 | 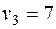 | 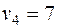 |
Решение 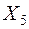 является оптимальным, так как все оценки клеток отрицательные. Значение целевой функции
является оптимальным, так как все оценки клеток отрицательные. Значение целевой функции 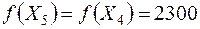 . Таким образом, мы получаем конечное оптимальное решение, отбрасывая фиктивного поставщика №4,
. Таким образом, мы получаем конечное оптимальное решение, отбрасывая фиктивного поставщика №4, 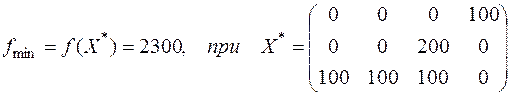 .
.
Задача №1. Решить задачу графически и симплекс-методом.
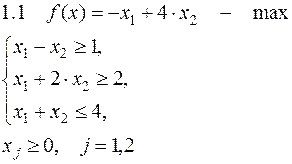 | 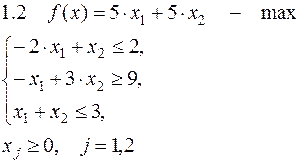 |
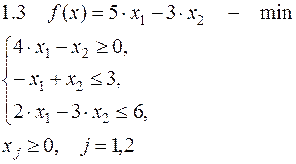 | 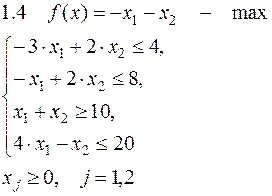 |
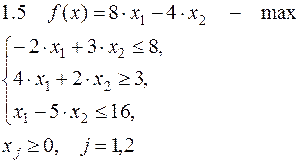 | 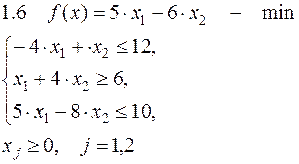 |
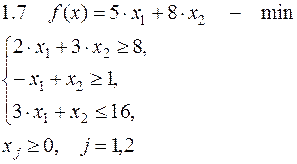 | 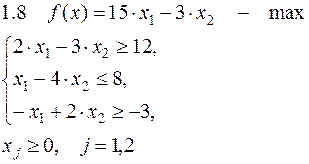 |
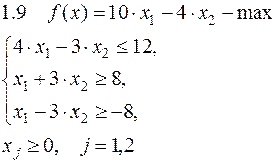 | 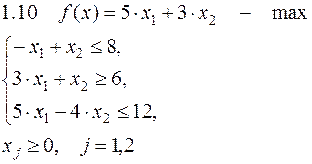 |
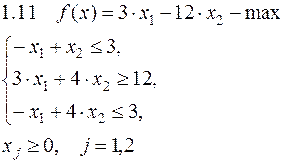 | 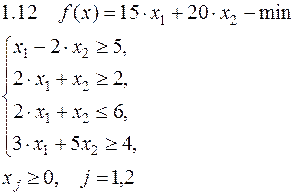 |
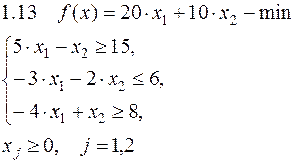 | 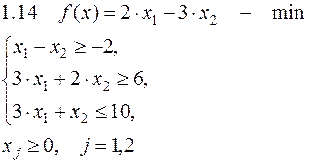 |
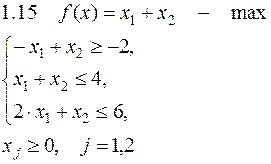 | 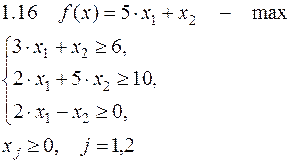 |
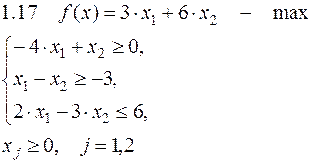 | 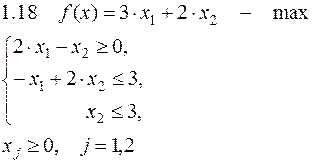 |
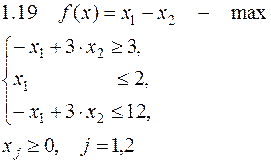 | 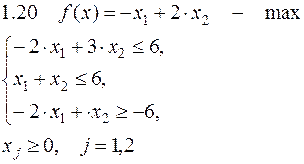 |
Задача №2. По условиям задачи составить ее математическую модель и найти оптимальный план с помощью симплекс-метода.
Вариант 1
Для сборки двух видов приборов α и β применяются три типа микросхем А, В, С. На один прибор α затрачивается одна микросхема А, три микросхемы В, а на один прибор β две микросхемы А и четыре С. Запас микросхем А и В по 30 штук, С – 40 штук. Сколько приборов каждого вида необходимо собрать для получения максимального дохода, если стоимость одного прибора α – 10 у.е., а β – 20 у.е.
Вариант 2
Строительная организация планирует сооружение домов типа D1 и D2 с однокомнатными, двухкомнатными и трёхкомнатными квартирами. Один дом D1 состоит из 30 однокомнатных, 10 двухкомнатных и 10 трёхкомнатных квартир. Для домов типа D2 эти данные равны соответственно 10, 40, 10. Годовой план ввода жилой площади составляет не менее 300 однокомнатных, 400 двухкомнатных и не более 400 трёхкомнатный квартир. Требуется составить программу строительства так, чтобы выполнить годовой план с наименьшими затратами, если известно, что затраты на возведение одного дома D1 составляют 100 млн. у.е, а D2 200 млн. у.е
Вариант 3
Для выращивания овощей по способу гидропоники необходима питательная смесь, содержащая не менее 55 единиц фосфора, 8 единиц азота, 32 единицы калия, не более 210 единиц смеси микроэлементов и не более 205 единиц магния. Для составления питательной смеси используют два вида удобрений А и В. Содержание указанных питательных веществ в 1 кг удобрений вида А составляет 5,1,11,16,17 единиц соответственно, вида В 11, 1, 3, 13, 12 единиц. Стоимость 1 кг удобрения каждого вида составляет 6у.е и 5 у.е. Сколько кг удобрений каждого вида надо взять, чтобы приготовить питательную смесь нужного состава при её минимальной стоимости?
Вариант 4
В мастерской при изготовлении шкафов и столов применяются три вида древесины. На один шкаф расходуется 0,2 м³ древесины первого вида, 0,8 м³ - второго и 0,5 м³ - третьего. На один стол 0,5м³, 0,5м³, 0,1м³ соответственно. В наличии имеется 20 м³ древесины первого вида, 40 м³ - второго и 30 м³ - третьего. Количество выпущенных шкафов и столов не запланировано. Прибыль мастерской от производства одного шкафа составляет 50 у.е., стола – 40 у.е. Сколько шкафов и столов должна изготовить мастерская, чтобы получить наибольшую прибыль?
Вариант 5
Хлебозавод выпускает кексы и сдобные булочки. Расход муки, сахара, изюма и других компонентов в центнерах на центнер каждого вида изделий приведён в таблице.
 сырьё Вид изд. сырьё Вид изд. | мука | сахар | изюм | Др. компон. |
| Сдоб. булочки | 0,3 | 0,2 | 0,1 | 0,2 |
| кексы | 0,4 | 0,1 | 0,7 | 0,5 |
Лимит сырья в центнерах, данный заводу на месяц, составляет соответственно 1240ц, 680ц, 64ц, 84ц. Сколько центнеров изделий каждого вида должен выпускать хлебозавод для получения максимальной прибыли, если при реализации 1ц сдобных булочек завод получает 6 у.е. прибыли, а кексов – 16 у.е.?
Вариант 6
На станках трёх типов А, В и С изготавливают изделия двух видов α и β. Для изготовления одного изделия первого вида используются в течение рабочего дня два станка типа А, один станок типа В и один станок типа С. Для изделий второго вида эти числа равны 1; 1; 3. Всего в цехе имеется 20 станков типа А, 12 станков типа В и 30 станков типа С. Прибыль от выпуска одного изделия α составляет 40 у.е., β – 50 у.е. Выпуск изделий α и β не запланирован. Сколько нужно ежедневно выпускать изделий каждого вида, чтобы получить максимальную прибыль?
Вариант 7
Пошивочный цех обувной фабрики изготавливает три вида обуви из заготовок пяти типов, поступающих из раскройного цеха. Расход заготовок на пару каждого типа приведён в таблице.
 Вид обуви сырьё Вид обуви сырьё | I | II | III |
| 1 тип 2 тип 3 тип 4 тип 5 тип |
Запас заготовок первого типа составляет 90 штук, второго – 60 штук, третьего – 120 штук, четвёртого – 130 штук, пятого – 40 штук. Сколько пар обуви каждого вида следует выпускать фабрике для получения максимальной прибыли, если при реализации одной пары обуви каждого вида она составляет 3 у.е., 5 у.е., 8 у.е. соответственно.
Вариант 8
Сухогруз грузоподъёмностью 1500т может принять груз пяти наименований А, В, С, D, Е общим объёмом не более 500м³. Вес в тоннах и объём в м³ единицы каждого вида груза составляет: 50, 100, 70, 90, 60т; 45, 30, 25, 45,40 м³. Стоимость единицы груза А – 1,5 тыс. у.е, В – 2 тыс. у.е., С – 1,3 тыс.у.е., D – 1,8 тыс. у.е., Е – 1,5 тыс. у.е. Загрузить судно грузом максимальной суммарной стоимости, если груза С должно быть поставлено не менее 15 единиц.
Вариант 9
Цех выпускает три вида столярных изделий с использованием трёх видов сырья, расход которого на единицу каждого вида изделий приведён в таблице.
 продукция сырьё продукция сырьё | I | II | III |
Запасы сырья каждого вида на планируемый период составляют 200, 320 и 400 единиц соответственно. План выпуска изделий каждого вида за этот период составляет 10, 20, 15 единиц. Сколько единиц изделий каждого вида необходимо выпускать для получения максимальной прибыли и выполнения плана, если прибыль, получаемая от реализации одного изделия каждого вида, составляет 6 у.е., 12 у.е. и 15 у.е.
Вариант 10
На приобретение оборудования для нового производственного участка имеются капиталовложения 21 тыс. у.е., а для его размещения выделена площадь 49 м². Можно приобрести оборудование двух видов. Единица оборудования первого вида занимает 7 м² и стоит 2 тыс. у.е. Для оборудования второго вида эти данные: 2 м² и 7 тыс. у.е. Прибыль от единицы нового оборудования составляет 4 тыс. у.е и 7 тыс.у.е соответственно. Сколько нужно приобрести нового оборудования каждого вида, чтобы получить наибольшую прибыль и при этом полностью израсходовать выделенные капиталовложения?
Вариант 11
В цехе химического производства для изготовления двух видов продукции А и В используется три типа сырья α, β и γ. На производство одного кг продукта А затрачивается 3 единицы сырья α, 8 единиц сырья β и 2 единицы – γ, а на один кг продукта В затрачивается 3 единицы сырья α, 3 единицы - β и 5 единиц – γ. Запасы сырья составляют α -57 ед, β – 96 ед и γ – 64 ед. Сколько кг продукции А и В необходимо изготовить для получения максимального дохода, если стоимость одного продукта А составляет 7 у.е., а В – 9 у.е.?
Вариант 12
Два вида продуктов А и В выпускаются с использованием трёх видов ресурсов α, β и γ. На один кг продукта А затрачивается 1 единица сырья α, 4 единицы сырья β и 3 единицы сырья γ, а на один кг продукта В затрачивается 3 единицы α, 3 единицы β и 3 единицы γ. Лимит ресурса α составляет 30 единиц, β – 48 единиц, γ – 60 единиц. Сколько кг продукции А и В необходимо изготовить для получения наибольшей прибыли, если стоимость одного продукта А составляет 7 у.е., а В – 9 у.е.?
Вариант 13
Столовая предприятия имеет 14 кг муки, 75 штук яиц, 11 кг маргарина, 6 кг сахарного песка и 10 кг сметаны. Расход этих продуктов на одно кондитерское изделие каждого вида указан в таблице (в кг).
| Вид изделия | мука | яйца | маргарин | сахар | сметана |
| Бисквитное песочное кекс | 0.2 0.5 1/3 | 25/3 | 0.5 1/3 | 0.2 0.15 1/3 | 0.5 |
Сколько кондитерских изделий каждого вида необходимо испечь, чтобы суммарное их количество было максимальным, а весь маргарин израсходован?
Вариант 14
Два вида продукции А и В выпускаются с помощью трёх технологических способов. При использовании I технологического способа выпускается 5 единиц продукции А и 3 единицы продукции В, при использовании II технологического способа 1 единица А и 5 единиц В, при использовании III технологического способа – 1 единица А и 1 единица В. По плану продукции, произведённой I технологическим способом должно быть не менее 30 единиц, II способом не менее 10 единиц, а III технологическим способом не более 8 единиц. Прибыль при реализации продукции составляет 1 у.е. и 5 у.е. соответственно. Сколько изделий А и В необходимо изготовить, чтобы получить максимальную прибыль?
Вариант 15
Школьная столовая готовит два вида тортов к выпускному вечеру: песочный (П) и бисквитно-кремовый (Б). Расход муки на единицу изделия торта П составляет 4 кг, а торта Б – 1 кг, яиц – 3 и 8 штук соответственно и по 1 кг маргарина. Планируется истратить не менее 8 кг муки, не менее 24 яиц и не более 6 кг маргарина. Сколько тортов каждого вида необходимо изготовить, чтобы получить максимальный доход, если стоимость торта П составляет 2 у.е., а торта Б – 7 у.е.?
Вариант 16
Для изготовления пластмассовых втулок и шестерёнок требуется стеклоткань, эпоксидная смола и отвердитель. На изготовление одной втулки затрачивается 4 единицы стеклоткани, 3 единицы эпоксидной смолы и 2 единицы отвердителя, а на изготовление одной шестерёнки – соответственно 3, 4 и 6 единиц материалов. Прибыль предприятия от изготовления одной втулки составляет 2 у.е., а шестерёнки – 4 у.е. Сколько втулок и шестерёнок должно изготовлять предприятие для получения наибольшей прибыли, если в его распоряжении имеется 480 единиц стеклоткани, 444 единиц эпоксидной смолы и 546 единиц отвердителя?
Вариант 17
Для выпуска изделий α и β предприятие имеет 120 единиц ресурса А, 89 единиц ресурса В и 200 единиц ресурса С. При производстве одной единицы изделия α затрачивается 1 единица ресурса А и 2 единицы ресурса С; для изделия β эти числа равны 1, 1, 1. Прибыль от реализации одного изделия α составляет 2 тыс. у.е., а β – 4 тыс. у.е. Найти оптимальный план выпуска продукции α и β в целях получения максимальной прибыли.
Вариант 18
Фабрика выпускает ткани двух типов α и β на станках типа I, II, III. Производительность станка типа I в час составляет для ткани α – 4м, для ткани β – 1м. Для станка типа II эти данные составляют: α – 4м, β – 3м, а для станка типа III: α – 4м, β – 15м. Фабрика должна производить за час не менее 20м ткани на станках I типа, не менее 40м ткани на станках типа II и не менее 88м ткани на станках типа III. Требуется выполнить план с наименьшими затратами, если известно, что затраты на производство одного метра тканей α и β составляют 6 и 10 у.е. соответственно.
Вариант 19
Студенческая столовая ежедневно готовит три варианта комплексных обедов: мясной по цене 100 руб, рыбный по цене 70 руб. и диетический по цене 60 руб. Суммарное количество реализованных обедов не превосходит 660, из них суммарное количество мясных и рыбных по крайней мере в 10 раз больше диетических, а количество мясных по крайней мере вдвое больше рыбных. Сколько комплексных обедов каждого вида должно быть приготовлено, чтобы суммарный кассовый сбор за них был максимальный?
Вариант 20
Для изготовления хромоникелевой стали можно использовать два вида руды. Одна тонна руды первого вида содержит в своём составе 2 единицы железа, 1 единицу хрома и 2 единицы никеля; для одной тонны руды второго вида содержание этих компонент составляет 4, 4, 5 и 3 соответственно. В сплаве должно содержаться не менее 20 единиц железа, не менее 15 единиц хрома и не менее 10 единиц никеля. Сколько руды каждого вида надо для изготовления наиболее дешёвого сплава, удовлетворяющего указанным условиям, если одна тонна руды первого вида стоит 4 денежных единицы, а второго – 10 денежных единиц?
Задача №3 «Транспортная задача». Построить опорный план методом минимальной стоимости и найти оптимальное решение задачи методом потенциалов.
| Вар. 1. | 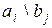 | Вар. 2. | 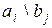 | ||||||
| 3. | 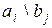 | 4. | 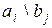 | ||||||
| 5. | 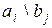 | 6. | 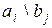 | ||||||
| 7. | 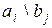 | 8. | 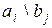 | ||||||
| 9. | 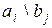 | 10. | 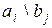 | ||||||
| Вар. 11. | 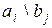 | Вар. 12. | 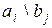 | ||||||
| 13. | 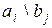 | 14. | 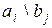 | ||||||
| 15. | 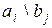 | 16. | 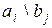 | ||||||
| 17. | 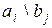 | 18. | 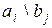 | ||||||
| 19. | 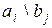 | 20. | 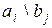 | ||||||
Задача №4. Найти кратчайший путь от вершины х0 до остальных вершин графа. Граф описывается перечнем всех своих дуг (верхняя строка) и их длинами (нижняя строка). Дуга хiх g с обозначается парой чисел i g.
| 01 02 04 12 13 23 35 36 37 41 45 51 56 511 67 610 78 79 710 89 910 1011 1012 1112 17 13 8 12 28 15 11 18 15 11 5 7 14 12 21 5 7 13 12 4 3 14 16 20 | Вар.1 | |
| 01 05 14 15 17 27 28 29 211 32 40 48 52 57 63 68 610 74 79 89 96 109 1012 119 12 23 12 13 31 10 33 15 14 20 15 13 4 18 19 8 21 12 15 16 19 19 8 17 | Вар.2
Подборка статей по вашей теме:
|
 2015-06-10
2015-06-10 4612
4612