Безмоментная теория оболочек

1.Определить поперечное перемещение 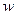в сферической оболочке, нагруженной внутренним давлением по безмоментной теории. Записать решение в виде общей формулы. Размеры оболочки и характеристики материала считать известными.

2.Определить линейные деформации в цилиндрической оболочке с днищами, нагруженной внутренним давлением по безмоментной теории. Записать решение в виде общих формул. Размеры оболочки и характеристики материала считать известными.

3.Определить линейные деформации в конической оболочке с днищами, нагруженной внутренним давлением по безмоментной теории. Записать решение в виде общих формул. Размеры оболочки и характеристики материала считать известными.

4.Определить максимальные значения внутренних силовых факторов в оболочке в форме кругового тора. Параметры оболочки считать известными.

5.Цилиндрическая оболочка с днищами, образованная однонаправленной намоткой стеклоленты, нагружена внутренним давлением. Пренебрегая жесткостью полимерного связующего определить оптимальный угол намотки ленты на цилиндрической части оболочки. Оболочку считать безмоментной. Будет ли оболочка в рамках принятых допущений кинематически неизменяемой?

6.Определить собственную частоту и форму нормированную по массе симметричных радиальных колебаний безмоментной сферической оболочки. Записать решение в виде общей формулы. Размеры оболочки и характеристики материала считать известными.

7.Определить собственную радиальных частоту радиальных колебаний безмоментной бесконечно длинной цилиндрической оболочки (кольцевую часототу). Записать решение в виде общей формулы. Размеры оболочки и характеристики материала считать известными.

8.Определить, возможно ли образование складок на поверхности мягкой оболочки в форме кругового тора, нагруженной внутренним давлением.

9.Оболочка закреплена в продольном направлении на левом торце и нагружена распределенной нагрузкой 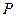на правом торце. Найти величину поперечного смещения 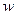, используя безмоментную теорию. Длина оболочки 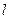, радиус 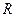, толщина 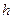. Модуль упругости материала оболочки 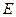, коэффициент Пуассона .

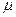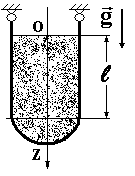
10.Цилиндрическая оболочка с полусферическим днищем заполнена жидкостью с плотностью 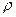. Длина цилиндрической части оболочки 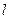, радиус 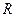, толщина 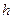. Модуль упругости материала оболочки 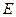, коэффициент Пуассона 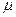. Найти внутренние силовые факторы в цилиндрической части оболочки, считая ее безмоментной. Продольное и окружное усилие представить в виде функции координаты 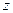. Начало координат 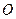выбрано на поверхности жидкости.

11.Цилиндрическая оболочка, закрепленная в тангенциальном направлении на левом торце, по правому торцу нагружена касательными силами, дающими в сумме крутящий момент 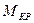. Считая, что оболочка находится в состоянии чистого сдвига, найдите касательные смещения 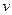на правом торце. Длина оболочки 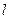, радиус 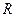, толщина 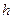. Модуль упругости материала оболочки 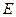, коэффициент Пуассона