2015-06-04
6119
Рассмотрим установившийся ламинарный поток в горизонтальной цилиндрической трубе на достаточном удалении от входа в неё.
Труба выбирается горизонтальной с целью исключения действия силы тяжести. При этом вывод упрощается, но результаты его справедливы для трубы, имеющей любой наклон.
Под достаточным удалением от входа понимается расстояние, превышающее длину начального участка, в пределах которого происходит формирование профиля скоростей. Таким образом, рассматривается установившийся равномерный поток, поскольку профиль скоростей по всей длине потока предполагается стабилизированным.
Поставим перед собой две задачи:
1) найти закон распределения местных скоростей в живом сечении потока;
2) определить величину гидравлических потерь на трение.
Решение этой задачи предполагает ответ на три вопроса:
1) Найти зависимость местной скорости от текущего радиуса точки -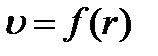 
;
2) Определить отношение максимальной скорости к средней по сечению -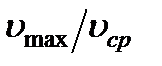 
.
3) Установить величину коэффициента, учитывающего неравномерность распределения местных скоростей -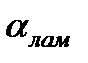 
.
Ламинарное течение является строго упорядоченным, слоистым течением без перемешивания жидкости. Теория ламинарного течения жидкости основывается на законе трения Ньютона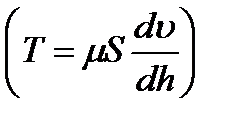 
. Это трение между слоями движущейся жидкости является единственным источником потерь энергии в данном случае.
Рассмотрим установившееся ламинарное течение жидкости в прямой круглой цилиндрической трубе с диаметром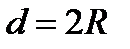 
(рис. 4.1).
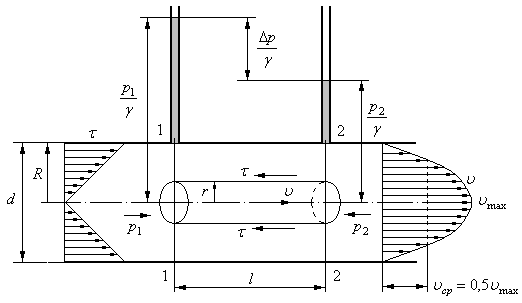
Рис. 4.1. К выводу закона распределения скоростей
и определению потерь при равномерном ламинарном течении
В потоке жидкости выделим цилиндрический объём длиной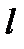 
и радиусом 
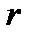, ограниченный с торцов двумя живыми сечениями потока 1-1 и 2-2.
Уравнение Бернулли для выбранных сечений примет вид
,
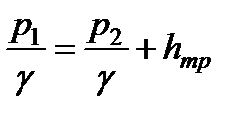где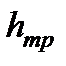 
- потери напора на трение по длине.
Отбросим остальную жидкость, и заменим её действие на выделенный цилиндрический объём соответствующими напряжениями. Спроектируем все внешние по отношению к этому объёму силы на направление потока. Такими внешними силами являются:
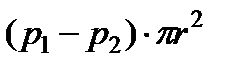- силы давления;
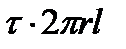- и силы сопротивления.
При равномерном течении жидкости сумма этих проекций должна быть равна нулю, т.к. ускорение при равномерном движении равняется нулю:
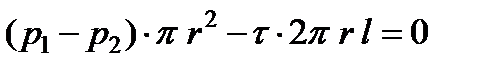, (4.1)
где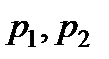 
- давление соответственно в сечениях 1-1 и 2-2;
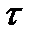- касательное напряжение на боковой поверхности.
Откуда касательное напряжение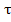 
равно
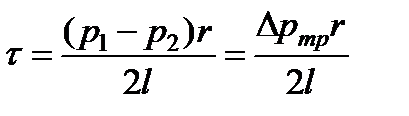, (4.2)
где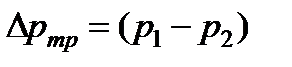 
- потери давления на трение.
Из формулы (4.14) следует, что касательные напряжения в поперечном сечении трубы изменяются по линейному закону (рис. 4.3) в функции радиуса и не зависят от режима движения жидкости.
При 
,
при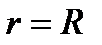 
.
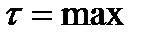Выразим касательное напряжение по закону Ньютона
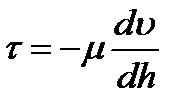. (4.3)
Знак минус обусловлен тем, что направление отсчёта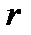 
(от оси к стенке вниз) противоположно направлению отсчёта 
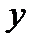(от стенки вверх).
Подставим значение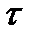 
в уравнение (4.2)
,
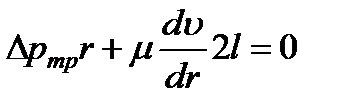Откуда
.
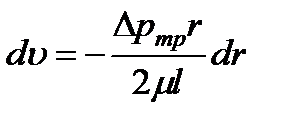После интегрирования, получим
.
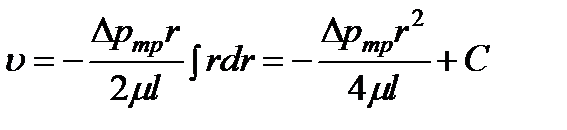Постоянную интегрирования С найдём при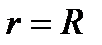 
, 
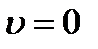
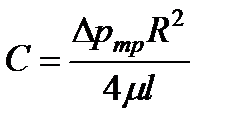. (4.4)
Тогда скорость по окружности радиусом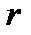 
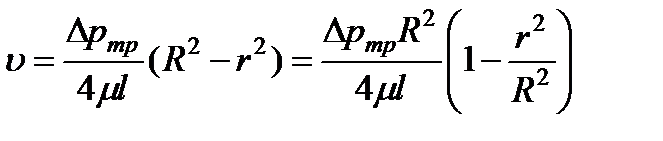. (4.5)
Учитывая, что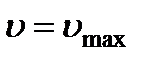 
при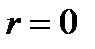 
, получим
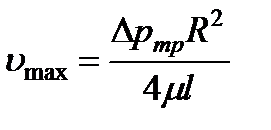, (4.6)
т.е. максимальная скорость совпадает с постоянной интегрирования (4.4).
Подставляем этот результат в формулу (4.5)
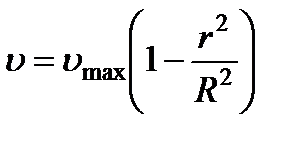. (4.7).
Формулы (4.5) и (4.7) выражают закон распределения скоростей по сечению круглой трубы при ламинарном течении, известного под названием закона Стокса.
Анализ этих выражений позволяет сделать вывод, что эпюра скоростей в живом сечении стабилизированного ламинарного потока (в круглой трубе) представляет собой параболоид вращения, а в проекции на плоскость – параболу второй степени (рис. 4.1).
