2015-06-04
8075
Числовые значения коэффициента трения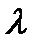 
и коэффициента местного сопротивления 
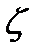зависят от режима течения и определяются в соответствии с законами гидродинамического подобия.
Для того чтобы потоки вязкой жидкости были между собой динамически подобны, необходимо кроме пропорциональности сходственных размеров и равенства соответствующих углов соблюдать равенство отношений инерционных сил к силам внутреннего трения, обусловленным вязкостью. Можно доказать (см. п. 3.15), что это условие означает равенство отношения
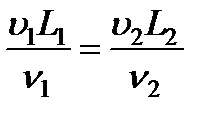. (3.50)
Здесь индексами 1 и 2 обозначены величины, относящиеся к каждому из двух сравниваемых потоков, причём под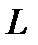 
понимается любой характерный для потока размер. Возможность произвольного выбора линейного размера вытекает из условия геометрического подобия потоков, означающего пропорциональность сходственных размеров
.
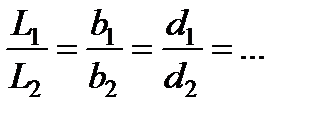Условие (3.504.2) может быть записано и как критерий подобия Рейнольдса
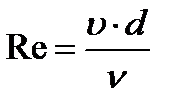. (3.51).
Для достижения динамического подобия потоков требуется соблюдение равенства чисел Рейнольдса
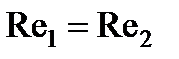или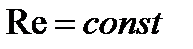 
.
Число Рейнольдса представляет собой меру отношения инерционных сил к силам внутреннего трения. Это критерий, учитывающий влияние вязкости на подобие.
При рассмотрении потока жидкости в круглой трубе в качестве характерного размера при определении числа Рейнольдса принимается внутренний диаметр трубы, а за скорость – средняя скорость потока (рис. 3.19,е)
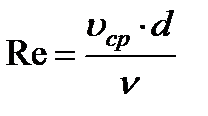. (3.52)
Для потока некруглого сечения при вычислении Re удобно в качестве характерного размера принимать так называемый гидравлический радиус
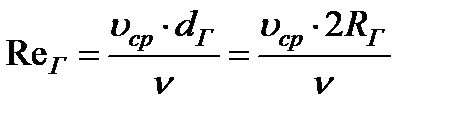. (3.53)
Гидравлическим радиусом называется отношение площади живого сечения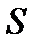 
к смоченному периметру 
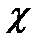(каппа)
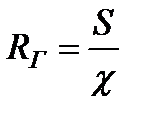. (3.54)
При прочих равных условиях (одинаковой скорости, одинаковой вязкости) совпадение гидравлических радиусов означает равенство отношений инерционных сил к силам внутреннего трения (поскольку инерционные силы зависят от площади сечения, а поверхность трения - от величины смоченного периметра).
Введение гидравлического радиуса как характерного размера при определении числа Рейнольдса позволяет сравнивать по критерию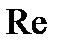 
потоки с разными формами живого сечения (рис. 3.19).
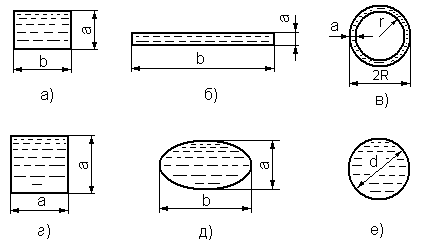
Рис.3.19. К определению гидравлического радиуса
при напорном течении
При напорном течении жидкости в прямоугольном канале (рис.3.19,а) гидравлический радиус
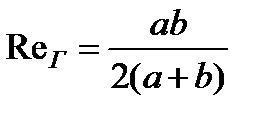. (3.55)
Для зазора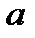 
(рис. 3.19,б), образованного параллельными стенками, когда 
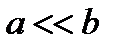, получим, пренебрегая слагаемым 
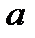в знаменателе правой части формулы (3.55)
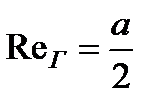. (3.56)
По этой же формуле определяется гидравлический радиус в случае кольцевого зазора, если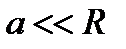 
(рис. 3.19,в).
При напорном течении в канале квадратного сечения (рис. 3.19, г)
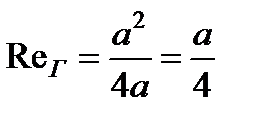. (3.57)
В случае эллиптического сечения (рис. 3.19, д)
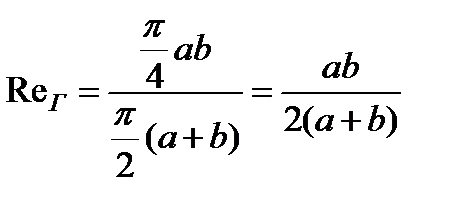. (3.58)
При напорном течении в круглой трубе (рис. 3.19,е)
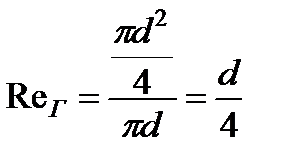. (3.59)
Таким образом, гидравлический радиус круглого сечения не совпадает с геометрическим - он не в два, а в четыре раза меньше геометрического диаметра. Следовательно, при переходе от числа Рейнольдса по гидравлическому радиусу к числу Рейнольдса по диаметру необходимо помнить, что
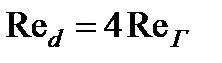. (3.60)
Следует также иметь в виду, что совпадение чисел Рейнольдса по гидравлическому радиусу у потоков с различными формами сечения не гарантирует в полной мере динамического подобия, так как в этом случае отсутствует подобие геометрическое.
