2.1. Поверхностный интеграл 1 рода.
2.1.1. Определение поверхностного интеграла 1 рода
Пусть в пространстве Оxyz дана поверхность  с площадью
с площадью 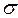 и в точках поверхности
и в точках поверхности  определена непрерывная функция f(x;y;z). Разобьем поверхность
определена непрерывная функция f(x;y;z). Разобьем поверхность  произвольные образом на n элементарных частей
произвольные образом на n элементарных частей 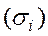 , площади которых
, площади которых 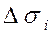 (i=1,2…,n). Выберем в каждой части
(i=1,2…,n). Выберем в каждой части 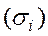 произвольную точку Mi (xi; yi; zi), найдем значение функции в этой точке
произвольную точку Mi (xi; yi; zi), найдем значение функции в этой точке 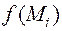 (рис.32).
(рис.32).
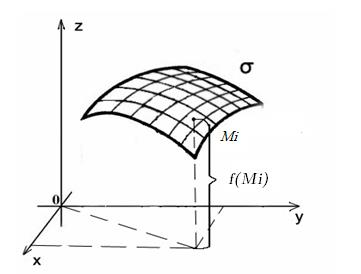
Рис.32
Составим интегральную сумму: 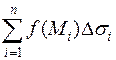 .
.
Обозначим через λ наибольший из диаметров элементарных областей 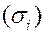 :
: 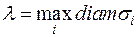 , где
, где 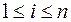 .
.
Если существует предел интегральной суммы 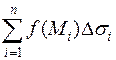 при
при 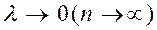 , не зависящий ни от способа разбиения поверхности
, не зависящий ни от способа разбиения поверхности  на элементарные части, ни от выбора точек Mi в элементарных частях, то этот предел называют поверхностным интегралом 1 рода от функции f(x;y;z) по поверхности
на элементарные части, ни от выбора точек Mi в элементарных частях, то этот предел называют поверхностным интегралом 1 рода от функции f(x;y;z) по поверхности  и обозначают:
и обозначают:
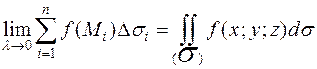
Физический смысл поверхностного интеграла 1 рода.
Если  - поверхность, с поверхностью плотностью
- поверхность, с поверхностью плотностью 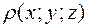 , то масса поверхности равна:
, то масса поверхности равна:
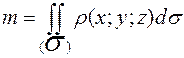 .
.
2.1.2. Основные свойства поверхностного интеграла 1 рода.
1. 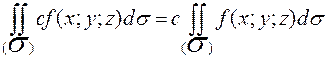
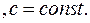
2. 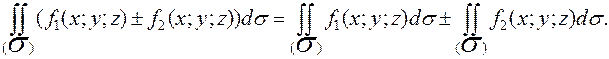
3.Если поверхность  разбита на
разбита на 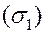 и
и 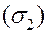 , такие, что
, такие, что 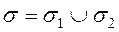 , а пересечение
, а пересечение 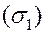 ,
, 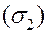 состоит из границы, их разделяющей, тогда
состоит из границы, их разделяющей, тогда
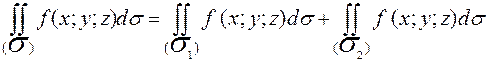
4. 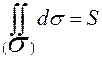 , где
, где 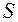 – площадь поверхности
– площадь поверхности  .
.
2.1.3. Вычисление поверхностного интеграла 1 рода.
Вычисление поверхностного интеграла 1 рода сводится к вычислению двойного интеграла по области (D)-проекции  на координатные плоскости.
на координатные плоскости.
1.Пусть поверхность  задана уравнением z=z(x;y). Тогда
задана уравнением z=z(x;y). Тогда
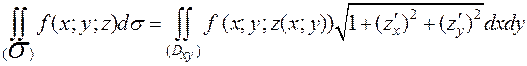 .
.
Где (Dxy) – проекция  на Оxy. То есть дифференциал вычисляется по формуле
на Оxy. То есть дифференциал вычисляется по формуле 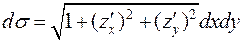 .
.
Отметим, что если поверхность  задана уравнением вида y=y(x;z) или x=x(y;z), то соответственно:
задана уравнением вида y=y(x;z) или x=x(y;z), то соответственно:
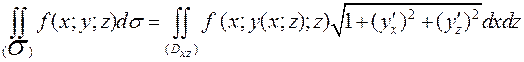 , то есть
, то есть 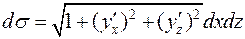 ,
,
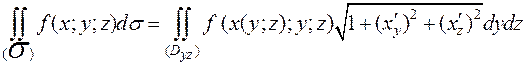 , то есть
, то есть 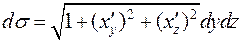 .
.
Где (Dxz), (Dyz) - проекции поверхности  на соответствующие координатные плоскости.
на соответствующие координатные плоскости.
Пример
Вычислить массу поверхности 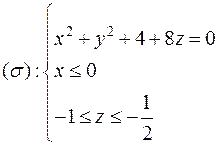 ,
,
с поверхностной плотностью 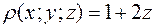 .
.
Решение
Массу поверхности найдем по формуле 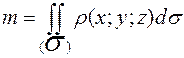 .
.
Рассмотрим поверхность 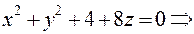
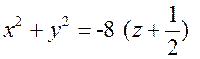 – это параболоид вращения со смещенной вершиной
– это параболоид вращения со смещенной вершиной 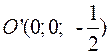 (рис.33).
(рис.33).
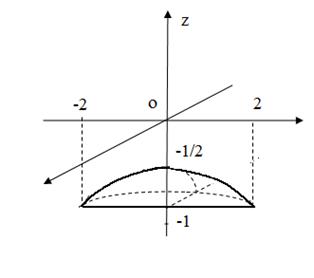
Рис.33
Очевидно, что 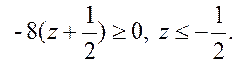
Выразим координату z из уравнения поверхности 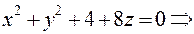
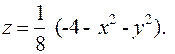
Так как поверхность задана уравнением z=z(x;y),то дифференциал найдем по формуле 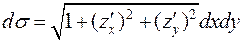 . Для этого найдём производные:
. Для этого найдём производные:
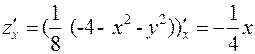 ,
, 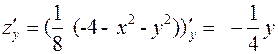 , тогда
, тогда 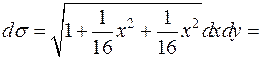
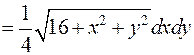 .
.
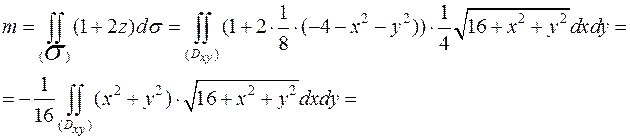 Вычисление поверхностного интеграла сведём к вычислению двойного интеграла, для этого рассмотрим проекцию поверхности в плоскость Oxy. Так как из условия задачи
Вычисление поверхностного интеграла сведём к вычислению двойного интеграла, для этого рассмотрим проекцию поверхности в плоскость Oxy. Так как из условия задачи 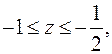 то при
то при 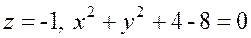 получим
получим 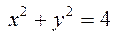 .
.
Таким образом, проекцией в плоскости Oxy является часть окружности 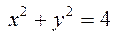 радиусом 2, где
радиусом 2, где 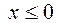 (рис.34).
(рис.34).
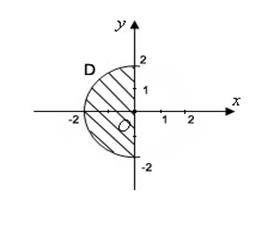
Рис.34
Для вычисления двойного интеграла перейдём к полярной системе координат.
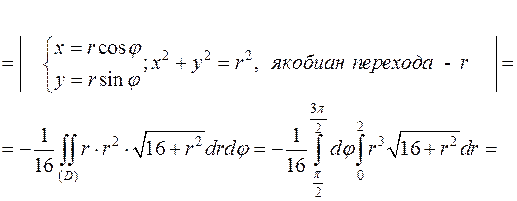

Вычислим сначала внутренний интеграл 
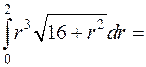
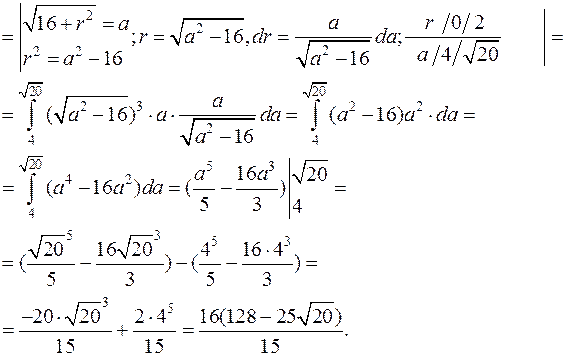
Тогда двойной интеграл равен
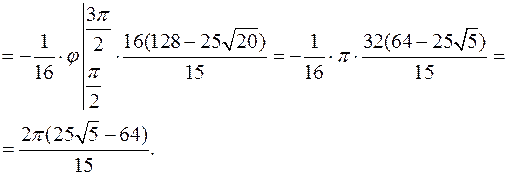
2.2Поверхностный интеграл 2 рода.
2.2.1. Определение поверхностного интеграла 2 рода
Пусть в пространстве Oxyz дана двусторонняя поверхность  Поверхность называется двусторонней, если после обхода такой поверхности, не пересекая её границы, направление нормали к ней не меняется (т.е. не меняется с внешнего направления на внутреннее и наоборот). Примером двусторонней поверхности является плоскость, эллипсоид, сфера и др. (рис.35).
Поверхность называется двусторонней, если после обхода такой поверхности, не пересекая её границы, направление нормали к ней не меняется (т.е. не меняется с внешнего направления на внутреннее и наоборот). Примером двусторонней поверхности является плоскость, эллипсоид, сфера и др. (рис.35).
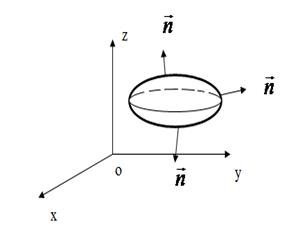
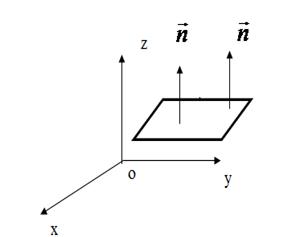
Рис.35
На двусторонней поверхности выбор направления нормали в одной точке однозначно определяет выбор направления нормали во всех точках поверхности. Поэтому двусторонние поверхности называют также ориентируемыми. Выбор определенной стороны поверхности называется ориентацией поверхности.
Пусть в точках поверхности  определена непрерывная функция f(x;y;z). Выберем определённую сторону поверхности, т.е. направление нормали. Выбранную сторону поверхности разобьем произвольным образом на n элементарных частей
определена непрерывная функция f(x;y;z). Выберем определённую сторону поверхности, т.е. направление нормали. Выбранную сторону поверхности разобьем произвольным образом на n элементарных частей 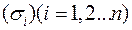 , спроецируем их на координатные плоскости. Обозначаем
, спроецируем их на координатные плоскости. Обозначаем 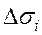 площадь проекции. В частности
площадь проекции. В частности 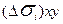 - площадь проекции элементарной части
- площадь проекции элементарной части 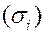 на координатную плоскость Oxy.
на координатную плоскость Oxy.
При этом площадь проекции 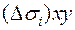 берем со знаком плюс, если выбрана верхняя (положительная относительно оси Oz) сторона поверхности, т.е. нормаль
берем со знаком плюс, если выбрана верхняя (положительная относительно оси Oz) сторона поверхности, т.е. нормаль 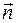 к выбранной стороне поверхности составляет с осью Oz острый угол
к выбранной стороне поверхности составляет с осью Oz острый угол 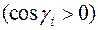 ; со знаком минус, если выбрана нижняя (отрицательная относительно оси Oz) сторона поверхности, т.е. угол нормали
; со знаком минус, если выбрана нижняя (отрицательная относительно оси Oz) сторона поверхности, т.е. угол нормали 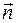 с осью Oz тупой
с осью Oz тупой 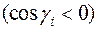 (рис.36).
(рис.36).
Выберем в каждой части 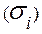 произвольную точку
произвольную точку
Mi (xi; yi; zi), найдем значение функции f(xi; yi; zi) в этой точке.
Составим интегральную сумму 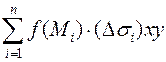 .
.
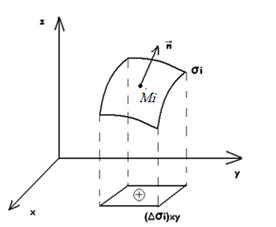
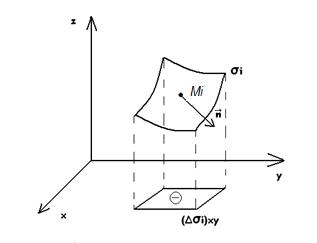
Рис.36
Обозначим через λ наибольший из диаметров элементарных частей 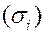 :
: 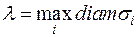 , где
, где 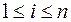 .
.
Если существует предел интегральной суммы 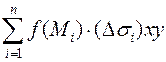 при
при 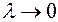
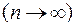 , не зависящий ни от способа разбиения поверхности
, не зависящий ни от способа разбиения поверхности  на элементарные части, ни от выбора точек
на элементарные части, ни от выбора точек 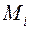 в каждой элементарной части, то этот предел называют поверхностным интегралом 2 рода относительно координат x, y от функции f(x;y;z) по поверхности
в каждой элементарной части, то этот предел называют поверхностным интегралом 2 рода относительно координат x, y от функции f(x;y;z) по поверхности  и обозначают:
и обозначают:
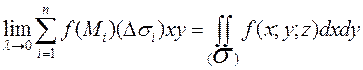 .
.
Аналогично определяют поверхностные интегралы 2 рода по переменным y и z; z и x.
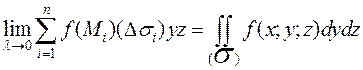 ,
, 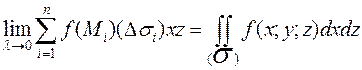 .
.
Если задано сразу три непрерывные функции 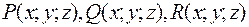 , определенные в точках двусторонней поверхности
, определенные в точках двусторонней поверхности  и от этих функций существуют интегралы
и от этих функций существуют интегралы 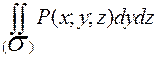 ,
, 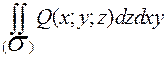 ,
, 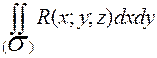 ,
,
то выражение:
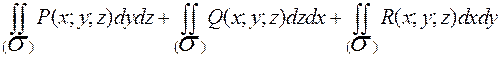 называют поверхностным интегралом 2 рода общего вида и записывают:
называют поверхностным интегралом 2 рода общего вида и записывают:
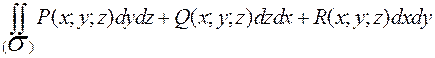 .
.
Если  – замкнутая поверхность, то поверхностный интеграл по внешней стороне обозначают
– замкнутая поверхность, то поверхностный интеграл по внешней стороне обозначают 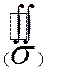 , по внутренней
, по внутренней 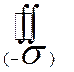 .
.
2.2.2. Основные свойства поверхностного интеграла 2 рода:
1. Поверхностный интеграл 2 рода меняет знак при перемене стороны поверхности 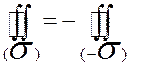 .
.
2. Постоянный множитель можно вынести за знак поверхностного интеграла 2 рода.
3. Поверхностный интеграл 2 рода от суммы функций равен сумме соответствующих поверхностных интегралов.
4. Поверхностный интеграл 2 рода по всей поверхности  , где
, где 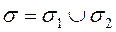 равен сумме интегралов по её частям
равен сумме интегралов по её частям 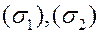 , если
, если 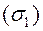 и
и 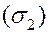 пересекаются лишь по границе, их разделяющей.
пересекаются лишь по границе, их разделяющей.
5. Если  - поверхность, образующие которой параллельны оси Ох, то:
- поверхность, образующие которой параллельны оси Ох, то:
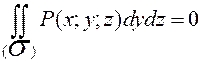 .
.
Аналогично, если образующие поверхности  параллельны осям Oz, Oy то соответственно:
параллельны осям Oz, Oy то соответственно:
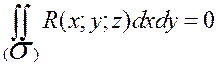 ,
, 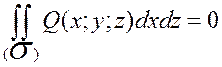
2.2.3. Вычисление поверхностного интеграла 2-го рода.
Вычисление поверхностного интеграла2-го рода сводится к вычислению двойного интеграла.
Пусть уравнение поверхности  z = z(x,y) и пусть нормаль
z = z(x,y) и пусть нормаль 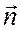 к поверхности
к поверхности  образует с осью Оz острый угол,
образует с осью Оz острый угол, 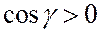
(в данном случае верхняя, положительная относительно оси Oz, сторона поверхности). Тогда
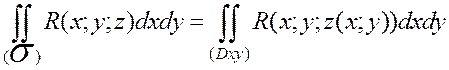 .
.
Если нормаль 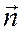 к поверхности
к поверхности  образует с осью Оz тупой угол,
образует с осью Оz тупой угол,
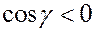 (в данном случае нижняя, отрицательная относительно оси Oz, сторона поверхности).
(в данном случае нижняя, отрицательная относительно оси Oz, сторона поверхности).
Тогда
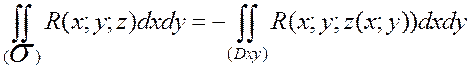 .
.
Аналогично, если поверхность  задана уравнением y=y(x;z), рассматриваем угол, который образует нормаль
задана уравнением y=y(x;z), рассматриваем угол, который образует нормаль 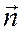 к поверхности
к поверхности  с осью Оy.
с осью Оy.
Знак перед интегралом выбираются в зависимости от ориентации поверхности, плюс - если нормаль образует с осью Оу острый угол (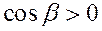 , положительная относительно оси Oy сторона поверхности), минус - угол тупой (
, положительная относительно оси Oy сторона поверхности), минус - угол тупой (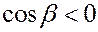 , отрицательная относительно оси Oy сторона поверхности). Тогда
, отрицательная относительно оси Oy сторона поверхности). Тогда
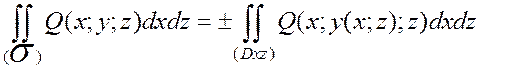 ,
,
где (Dxz) - проекция поверхности  на координатную плоскость Оxz.
на координатную плоскость Оxz.
Аналогично, если поверхность  задана уравнением x=x(y;z), рассматриваем угол, который образует нормаль
задана уравнением x=x(y;z), рассматриваем угол, который образует нормаль 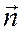 к поверхности
к поверхности  с осью Ох. Знак перед интегралом выбирают в зависимости от ориентации поверхности, плюс - если нормаль образует с осью Ох острый угол (
с осью Ох. Знак перед интегралом выбирают в зависимости от ориентации поверхности, плюс - если нормаль образует с осью Ох острый угол (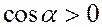 , положительная относительно оси Ox сторона поверхности), минус - угол тупой
, положительная относительно оси Ox сторона поверхности), минус - угол тупой
(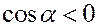 , отрицательная относительно оси Ox сторона поверхности). Тогда:
, отрицательная относительно оси Ox сторона поверхности). Тогда:
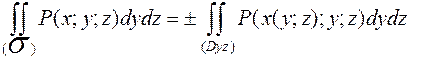 ,
,
где (Dyz)- проекция поверхности  на координатную плоскость Oyz.
на координатную плоскость Oyz.
При вычислении поверхностного интеграла общего вида используют формулу (метод проекций):
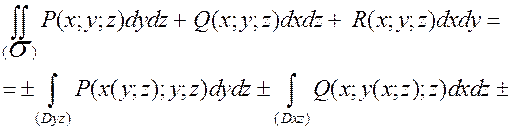
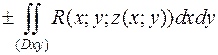 .
.
Пример
Вычислить интеграл: 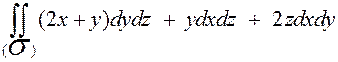 , где
, где  - верхняя сторона поверхности
- верхняя сторона поверхности 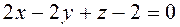 , отсечённая плоскостями
, отсечённая плоскостями 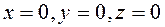 .
.
Решение
Построим часть плоскости 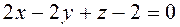 , отсечённую плоскостями
, отсечённую плоскостями 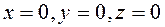 (рис.37).
(рис.37).
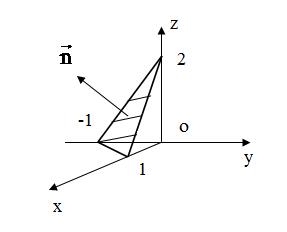
Рис.37
Применим метод проекций на координатные плоскости. Очевидно, что при переходе к двойным интегралам из уравнения плоскости 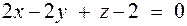 для первого двойного интеграла в подынтегральной функции следует исключить переменную
для первого двойного интеграла в подынтегральной функции следует исключить переменную 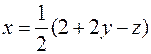 , для второго - переменную
, для второго - переменную 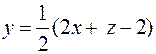 , для третьего - переменную
, для третьего - переменную 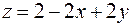 .
.
Для определения знака перед двойными интегралами рассмотрим углы нормали к поверхности с координатными осями.
Координаты вектора нормали плоскости 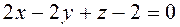 ,
,
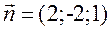 , модуль вектора
, модуль вектора 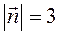 .
.
Соответственно, направляющие косинусы 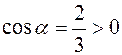 ,
, 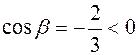
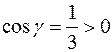 . Таким образом, нормаль образует с осью Ох, осью Оz острые углы, а с осью Оу – тупой угол
. Таким образом, нормаль образует с осью Ох, осью Оz острые углы, а с осью Оу – тупой угол
(рассматриваем верхнюю сторону поверхности, (рис. 37)). Соответственно, перед первым и третьим двойным интегралом берём знак плюс, перед вторым - минус.
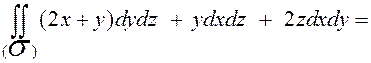
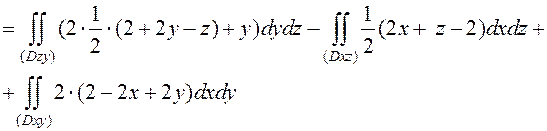
Для вычисления двойных интегралов рассмотрим проекции части плоскости 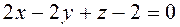 на координатные плоскости:
на координатные плоскости:
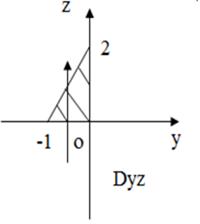 Рис.38 Рис.38 | 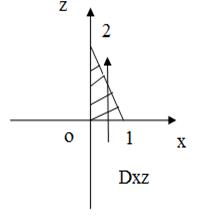 | 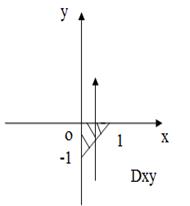 |
| на Oyz (x = 0) -2y + z – 2 = 0, z = 2+2y; | на Oxz (y = 0) 2x + z – 2 = 0 z = 2 – 2x; | на Oxy (z = 0) 2x – 2y – 2 = 0, y = x – 1; |
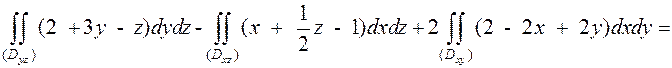
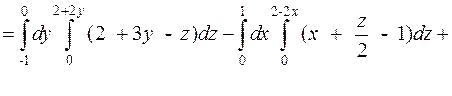
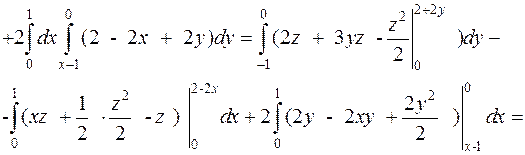
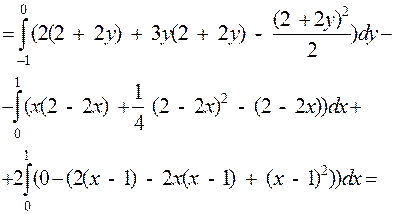
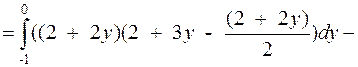
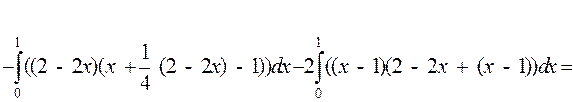
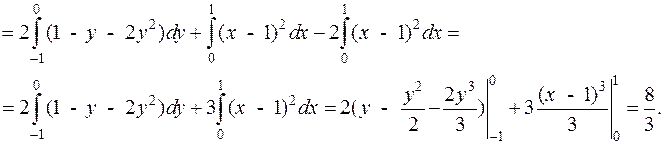 Пример
Пример
Вычислить интеграл 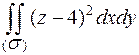 по нижней стороне полусферы
по нижней стороне полусферы 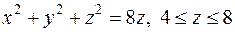 .
.
Решение
Преобразуем уравнение сферы 
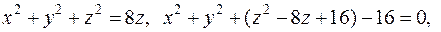
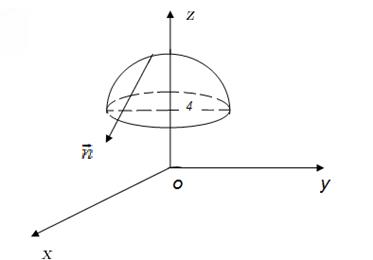
Рис.39
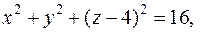
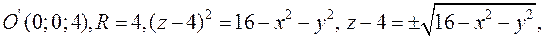 так как
так как 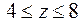 , то рассматриваем полусферу
, то рассматриваем полусферу 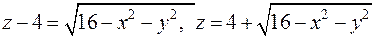 (рис.39).
(рис.39).
Спроецируем поверхность в плоскость Oxy. Для этого рассмотрим сечение плоскостью z=4.
При z=4 получим 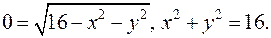 Проекцией поверхности в плоскость Oxy является круг радиусом 4.
Проекцией поверхности в плоскость Oxy является круг радиусом 4.
Очевидно, что нормаль к нижней (отрицательной относительно оси Oz стороне поверхности) стороне образует с осью Oz тупой угол, поэтому выбираем перед двойным интегралом знак минус. Для вычисления двойного интеграла перейдем к полярным координатам.
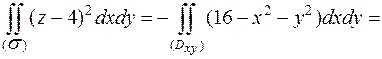
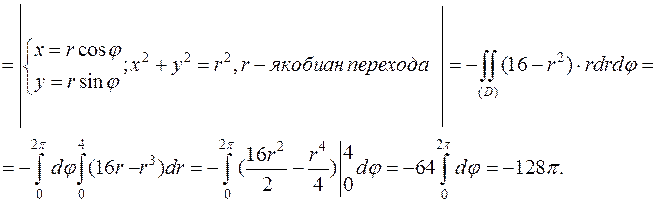
2.2.4. Формула связи между поверхностными интегралами 1 и 2 рода.
Поверхностные интегралы 1 и 2 рода связаны следующей формулой:
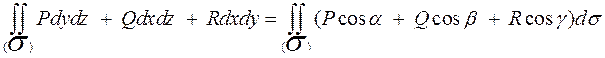
Где 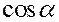 ,
, 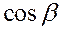 ,
, 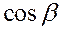 – направляющие косинусы нормали
– направляющие косинусы нормали 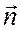 к выбранной стороне поверхности
к выбранной стороне поверхности  .
.
Пусть незамкнутая поверхность  задана уравнением
задана уравнением 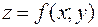 (поверхность однозначно проектируется на плоскость Oxy).
(поверхность однозначно проектируется на плоскость Oxy).
Тогда, если 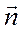 - нормаль к верхней (положительной относительно оси Oz) стороне поверхности, то её координаты
- нормаль к верхней (положительной относительно оси Oz) стороне поверхности, то её координаты 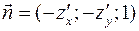 и соответственно направляющие косинусы равны:
и соответственно направляющие косинусы равны:
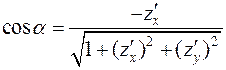 ;
;
 ;
;
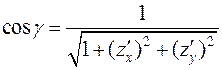 .
.
Если 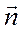 - нормаль к нижней (отрицательной относительно оси Oz) стороне поверхности, то её координаты
- нормаль к нижней (отрицательной относительно оси Oz) стороне поверхности, то её координаты  и соответственно направляющие косинусы равны:
и соответственно направляющие косинусы равны:
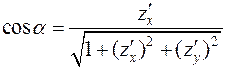 ;
;
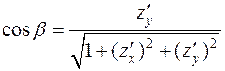 ;
;
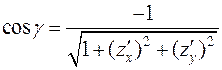 .
.
Пусть незамкнутая поверхность  задана уравнением
задана уравнением 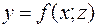 (поверхность однозначно проектируется на плоскость Oxz).
(поверхность однозначно проектируется на плоскость Oxz).
Тогда, если 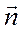 - нормаль к положительной относительно оси Oy стороне поверхности (угол с Oy острый), то её координаты
- нормаль к положительной относительно оси Oy стороне поверхности (угол с Oy острый), то её координаты 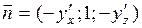 и соответственно направляющие косинусы равны:
и соответственно направляющие косинусы равны:
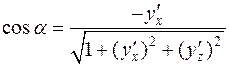 ;
;
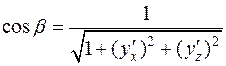 ;
;
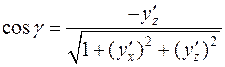 .
.
Если 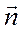 - нормаль к отрицательной относительно оси Oy стороне поверхности (угол с Oy тупой), то её координаты
- нормаль к отрицательной относительно оси Oy стороне поверхности (угол с Oy тупой), то её координаты 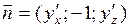 и соответственно направляющие косинусы равны:
и соответственно направляющие косинусы равны:
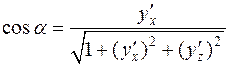 ;
;
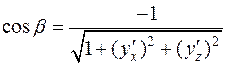 ;
;
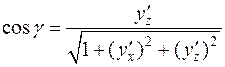 .
.
Аналогичные рассуждения можно привести для случая задания поверхности уравнением 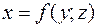 .
.
В главе поверхностный интеграл 1 рода, в случае задания функции уравнением 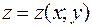 дифференциал находили по формуле
дифференциал находили по формуле 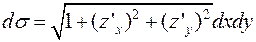 .
.
Таким образом, из формулы связи поверхностного интеграла 1 рода и 2 рода, если выбрана верхняя (положительная) сторона поверхности  , применяя формулы для нахождения дифференциала и направляющих косинусов получим:
, применяя формулы для нахождения дифференциала и направляющих косинусов получим:
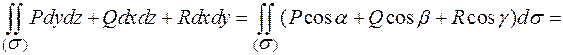
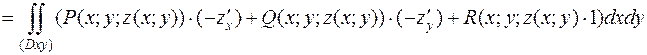 И, если выбрана нижняя (отрицательная) сторона поверхности
И, если выбрана нижняя (отрицательная) сторона поверхности  :
:
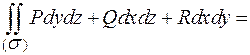
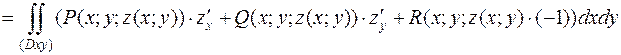
Аналогичные формулы можно получить для случая задания поверхности  уравнением
уравнением 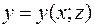 (
(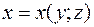 ), при этом, рассматривая положительную и отрицательную сторону поверхности относительно соответственно оси Oy (Ox).
), при этом, рассматривая положительную и отрицательную сторону поверхности относительно соответственно оси Oy (Ox).
Замечание. Предложенные формулы избавляют от необходимости проецировать поверхность на все три координатные плоскости
(следует только следить за однозначностью проецирования в соответственную координатную плоскость).
Пример
Вычислить 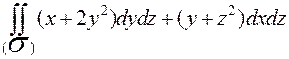 , где
, где  верхняя сторона поверхности
верхняя сторона поверхности 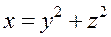 , отсечённая плоскостями
, отсечённая плоскостями 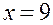 ,
, 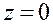 .
.
Решение
Построим поверхность 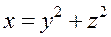 , отсечённую плоскостями
, отсечённую плоскостями 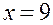 ,
, 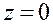 . Поверхность
. Поверхность 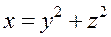 - параболоид вращения.
- параболоид вращения.
Для наглядности построения поверхность изобразим в левой системе координат.
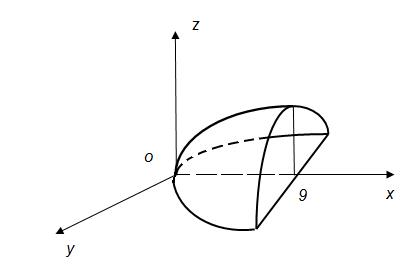
Рис.40
Верхняя часть параболоида однозначно проецируется как на плоскость Оxy, так и на Оyz, а на плоскость Оxz поверхность проецируется не однозначно (происходит наложение областей).
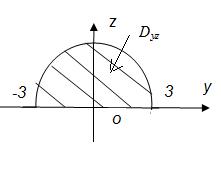
Рис.41
Спроецируем на плоскость Оyz (рис.41).
Поверхность 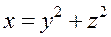 отсечена плоскостью
отсечена плоскостью 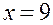 , тогда проекция на плоскость Оyz (Dyz):
, тогда проекция на плоскость Оyz (Dyz): 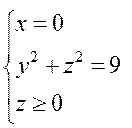 .
.
Координаты вектора нормали к верхней, в данном примере, отрицательной относительно оси Оx стороне поверхности 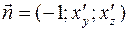 .Соответственно интеграл вычисляем по формуле:
.Соответственно интеграл вычисляем по формуле:
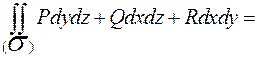
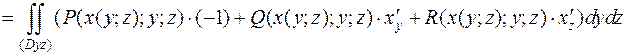 Найдём производные:
Найдём производные:
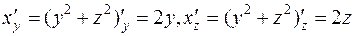 .
.
Следовательно 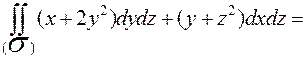
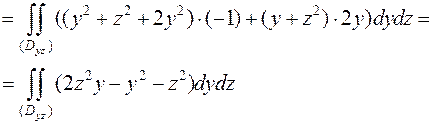
Вычислим двойной интеграл в полярной системе координат, в данном примере она задаётся: 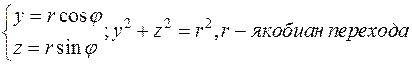 .
.
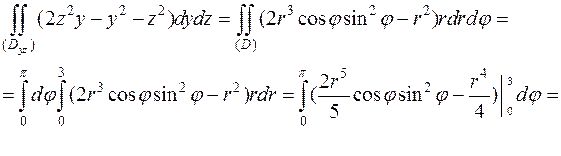
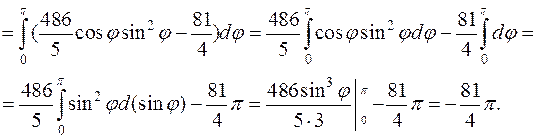
2.3. Формула Стокса.
Связь между криволинейным и поверхностным интегралами 2 рода.
Теорема. Пусть на ориентированной поверхности  заданы функции P(x;y;z), Q(x;y;z); R(x;y;z) – непрерывные весте со своими частными производными, тогда справедлива формула:
заданы функции P(x;y;z), Q(x;y;z); R(x;y;z) – непрерывные весте со своими частными производными, тогда справедлива формула:
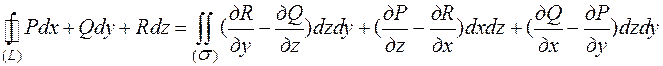 - формула Стокса.
- формула Стокса.
Где (L)- граница поверхности  и интегрирование вдоль (L) производится в положительном направлении (при обходе (L) поверхность остаётся слева) (рис.42).
и интегрирование вдоль (L) производится в положительном направлении (при обходе (L) поверхность остаётся слева) (рис.42).
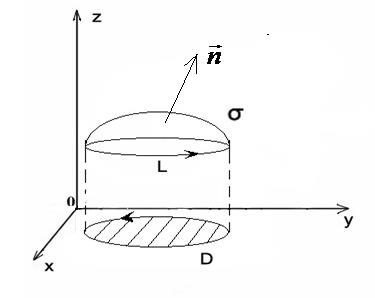
Рис.42
Пример
Вычислить интеграл 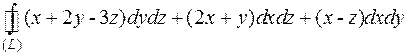 по контуру треугольника полученного в пересечении плоскости
по контуру треугольника полученного в пересечении плоскости 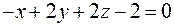 с координатными плоскостями (направление обхода положительное).
с координатными плоскостями (направление обхода положительное).
Решение
Построим контур треугольника (рис.43).
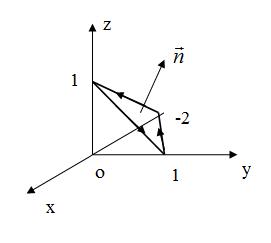
Рис.43
Так как контур замкнутый, то используем формулу Стокса (очевидно, что нормаль проведена к верхней стороне поверхности и направление обхода контура положительное).
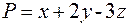 ,
, 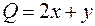 ,
, 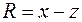 .
.
Тогда 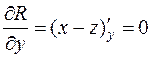 ,
, 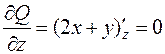 ,
, 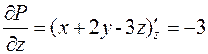 ,
, 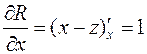 ,
, 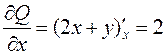 ,
, 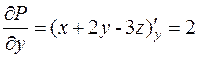 . Тогда
. Тогда
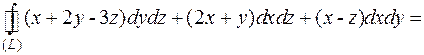
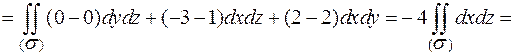
Сведём поверхностный интеграл к двойному интегралу.
Заметим, что угол нормали к плоскости с осью Оу острый, поэтому перед двойным интегралом выбираем знак плюс и интеграл равен площади проекции (Dxz) (смотри свойства двойного интеграла) (рис.44).
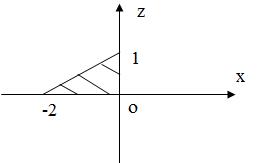
Рис.44
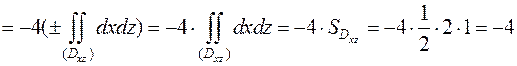
2.4. Формула Остроградского-Гаусса.
Связь между поверхностным интегралом 2 рода по замкнутой поверхности  и тройным интегралом по объёму, ограничивающему эту поверхность.
и тройным интегралом по объёму, ограничивающему эту поверхность.
Теорема. Пусть на ориентированной поверхности  заданы функции P(x;y;z), Q(x;y;z); R(x;y;z) – непрерывные вместе со своими частными производными, тогда справедлива формула:
заданы функции P(x;y;z), Q(x;y;z); R(x;y;z) – непрерывные вместе со своими частными производными, тогда справедлива формула:
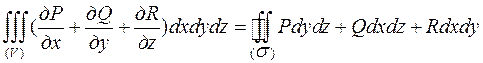
-формула Остроградского-Гаусса.
Где  - граница области (V) и интегрирование ведётся по внешней стороне поверхности
- граница области (V) и интегрирование ведётся по внешней стороне поверхности  (рис.45).
(рис.45).
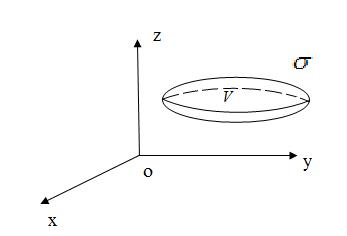
Рис.45
Пример
Вычислить
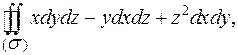 по внешней стороне замкнутой поверхности
по внешней стороне замкнутой поверхности  , состоящей из параболоида
, состоящей из параболоида 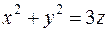 и сферы
и сферы 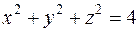 .
.
Решение
Так как поверхность замкнута, то используем формулу Остроградского-Гаусса (рис.46).
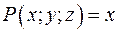 ,
, 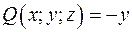 ,
, 
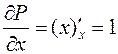 ,
, 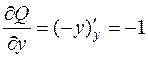 ,
, 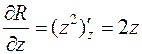 .
.
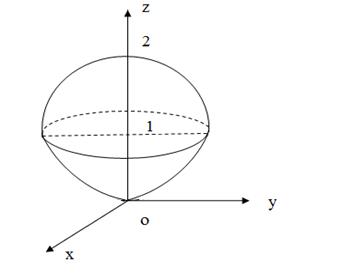
Рис.46
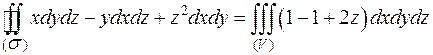
Найдём линию пересечения поверхностей:
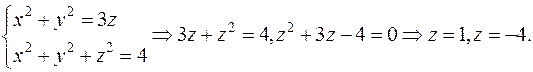
Линией пересечения является окружность 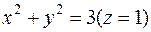 ,
, 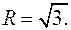 Вычислим тройной интеграл в цилиндрических координатах.
Вычислим тройной интеграл в цилиндрических координатах.
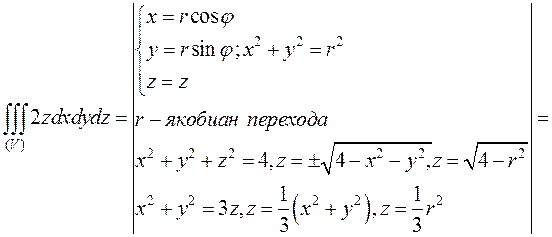
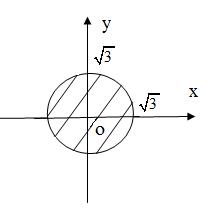
Рис.47
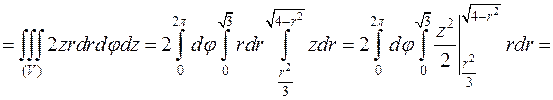
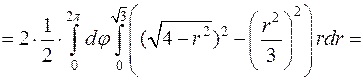
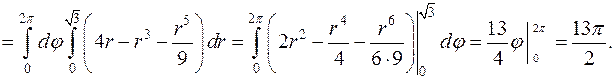 .
.
 2015-06-04
2015-06-04 9571
9571