| Вариант | |||||||
| Систе ма | х1+х2+х3=0 2х1-3х2+4х3=0 4х1-11х2+10х3=0 | 3х1-х2+2х3=0 х1+х2+х3=0 х1+3х2+3х3=0 | х1+3х2+2х3=0 2х1-х2+3х3=0 3х1-5х2+4х3=0 | 4х1-х2+10х3=0 х1+2х2-х3=0 2х1-3х2+4х3=0 | 2х1+5х2+х3=0 4х1+6х2+3х3=0 х1-х2-2х3=0 | 3х1-х2-3х3=0 2х1+3х2+х3=0 х1+х2+3х3=0 | х1-х2+2х3=0 2х1+х2-3х3=0 3х1+2х3=0 |
| Вариант | |||||||
| Систе ма | 2х1-х2-5х3=0 х1+2х2-3х3=0 5х1+х2+4х3=0 | 5х1-5х2+4х3=0 3х1+х2+3х3=0 х1+7х2-х3=0 | х1+3х2-х3=0 2х1+5х2-2х3=0 х1+х2+5х3=0 | 2х1+х2+3х3=0 3х1-х2+2х3=0 х1+3х2+4х3=0 | х1-2х2-х3=0 2х1+3х2+2х3=0 3х1-2х2+5х3=0 | 2х1+х2-х3=0 3х1-2х2+4х3=0 х1-5х2+3х3=0 | 4х1+х2+3х3=0 8х1-х2+7х3=0 2х1+4х2-5х3=0 |
| Вариант | |||||||
| Систе ма | х1+4х2-3х3=0 2х1+5х2+х3=0 х1-7х2+2х3=0 | х1-2х2+х3=0 3х1+х2+2х3=0 2х1-3х2+5х3=0 | х1+2х2+3х3=0 2х1-х2-х3=0 3х1+3х2+2х3=0 | 3х1+2х2=0 х1-х2+2х3=0 4х1-2х2+5х3=0 | 2х1-х2+3х3=0 х1+2х2-5х3=0 3х1+х2+х3=0 | 3х1+2х2-х3=0 2х1-х2+3х3=0 4х1+3х2+4х3=0 | х1-3х2-4х3=0 5х1-8х2-2х3=0 2х1+х2-х3=0 |
| Вариант | |||||||
| Систе ма | 3х1+5х2-х3=0 2х1+4х2-3х3=0 х1-3х2+х3=0 | 3х1-2х2+х3=0 2х1-3х2+2х3=0 4х1+х2-4х3=0 | 7х1+х2-3х3=0 3х1-2х2+3х3=0 х1-х2+2х3=0 | х1+2х2-4х3=0 2х1-х2-3х3=0 х1+3х2+х3=0 | 7х1-6х2+х3=0 4х1+5х2=0 х1-2х2+3х3=0 | 5х1-4х2+2х3=0 3х2-2х3=0 4х1+х2-3х3=0 | 6х1+5х2-4х3=0 х1+х2-х3=0 3х1+4х2+3х3=0 |
| Вариант | ||
| Систе ма | 8х1+х2-3х3=0 х1+5х2+х3=0 4х1-7х2+2х3=0 | х1+7х2-3х3=0 3х1-5х2+х3=0 3х1+4х2-2х3=0 |
Задание 10. На плоскости относительного некоторого базиса даны координаты трех векторов:
При N – четном: 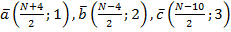
При N – нечетном: 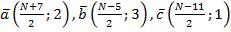 .
.
N- номер варианта по списку.
- Найти координаты векторов
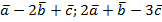 .
. - Проверить, что векторы
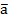 и
и 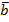 образуют базис на плоскости. Найти координаты вектора
образуют базис на плоскости. Найти координаты вектора 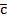 в этом базисе.
в этом базисе. - Определить при каком значении параметра α векторы
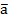 и
и 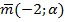 будут коллинеарными.
будут коллинеарными. - Найти координаты вектора
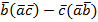
- Вычислить
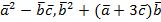
- Найти косинус угла между векторами
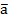 и
и 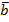 .
.
 2015-06-14
2015-06-14 645
645








