2015-06-14
280
Контрольная работа предусмотрена только для студентов заочной формы обучения. Для каждой контрольной работы приведено тридцать вариантов заданий. Студент должен выполнить вариант, номер которого совпадает с двумя последними цифрами номера его зачетной книжки. В начале работы следует привести полностью задание и исходные данные, а в конце – список используемой литературы.
Оформляется контрольная работа в ученической тетради рукописным способом, либо печатается на компьютере на стандартных листах формата А4. Графики выполняются с соблюдением требований ЕСКД и следуют по ходу изложения текстового и расчетного материала. Работа предоставляется в деканат не менее, чем за пятнадцать дней до начала экзаменационной сессии. Неряшливо оформленные работы могут быть возвращены студенту без рецензирования. В случае существенных замечаний работа отправляется на доработку. Если замечаний нет, а также при несущественных замечаниях, работа допускается к защите.
Расчеты в контрольной работе можно полностью выполнять вручную, либо частично с использованием ЭВМ. В разделе 4 «Компьютерное моделирование САУ» конспективно излагаются некоторые способы и методы моделирования систем автоматического управления с помощью пакета Matlab.
Исходные данные к контрольной работе
Структурная схема линейной САУ представлена на рисунке 1, где соответствующие передаточные функции имеют вид апериодических звеньев:
; 
; 
.
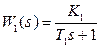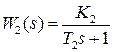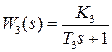Параметры Т 1, Т 2, Т 3, K 1, K 3 для каждого варианта задания представлены в таблице 2. Величина коэффициента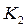 
выбирается далее из условия устойчивости.
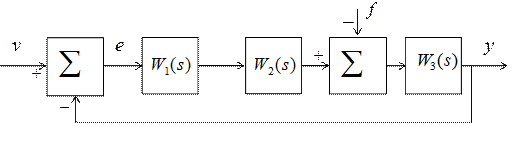
Рисунок 1
Варианты задания приведены в таблице 2.
Таблица 2
| Номер варианта | T 1 | T 2 | T 3 | K 1 | K 3 |
| 0,01 | 0,2 | 0,06 | 16,5 | ||
| 0,02 | 0,3 | 0,07 | 1,1 | ||
| 0,03 | 0,4 | 0,08 | 15,5 | 1,2 | |
| 0,04 | 0,5 | 0,09 | 1,3 | ||
| 0,05 | 0,6 | 0,1 | 14,5 | 1,4 | |
| 0,06 | 0,7 | 0,15 | 1,5 | ||
| 0,07 | 0,8 | 0,2 | 13,5 | 1,6 | |
| 0,08 | 0,9 | 0,25 | 1,7 | ||
| 0,09 | 0,3 | 12,5 | 1,8 | ||
| 0,05 | 1,1 | 0,15 | 1,9 | ||
| 0,06 | 1,2 | 0,2 | 11,5 | ||
| 0,07 | 1,3 | 0,25 | 2,1 | ||
| 0,08 | 1,4 | 0,3 | 10,5 | 2,2 | |
| 0,09 | 1,5 | 0,35 | 2,3 | ||
| 0,1 | 1,6 | 0,4 | 9,5 | 2,4 | |
| 0,01 | 0,2 | 0,1 | 2,5 | ||
| 0,02 | 0,3 | 0,2 | 8,5 | 2,6 | |
| 0,03 | 0,4 | 0,3 | 2,7 | ||
| 0,04 | 0,5 | 0,4 | 7,5 | 2,8 | |
| 0,05 | 0,6 | 0,5 | 2,9 | ||
| 0,06 | 0,7 | 0,6 | 6,5 | ||
| 0,07 | 0,8 | 0,7 | 3,1 | ||
| 0,08 | 0,9 | 0,8 | 5,5 | 3,2 | |
| 0,09 | 0,9 | 3,3 | |||
| 0,1 | 1,1 | 0,4 | 4,5 | 3,4 | |
| 0,2 | 1,2 | 0,5 | 3,5 | ||
| 0,3 | 1,3 | 0,6 | 3,5 | 3,6 | |
| 0,4 | 1,4 | 0,7 | 3,7 | ||
| 0,5 | 1,5 | 0,8 | 2,5 | 3,8 | |
| 0,6 | 1,6 | 0,9 | 3,9 |
Задание
1. Найти передаточные функции разомкнутой и замкнутой системы: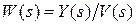 
при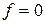 
, 
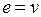(т.е. разомкнута главная обратная связь); 
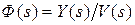при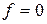 
- главная передаточная функция замкнутой системы; 
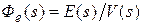при 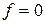- передаточная функция замкнутой системы по ошибке; 
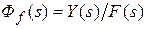при 
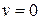- передаточная функция замкнутой системы по возмущению. Параметры 
, 
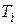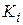входят в передаточные функции в общем виде, т.е. в буквенных символах.
2. Найти характеристическое уравнение замкнутой системы. Используя критерий Гурвица, записать в общем виде условия устойчивости. При заданных в таблице 2 параметрах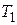 
, 
, 
, 
, 
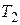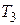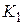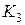найти максимальное граничное значение коэффициента передачи 
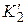при котором система еще устойчива. В дальнейшем полагать 
.
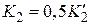3. Найти аналитические выражения и построить графики:
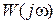– амплитудно-фазовой частотной характеристики (АФЧХ) разомкнутой системы;
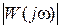– амплитудно-частотной характеристики (АЧХ) разомкнутой системы;
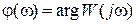– фазо-частотной характеристики (ФЧХ) разомкнутой системы;
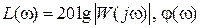− логарифмических амплитудно- и фазо-час-тотных характеристик (ЛАЧХ и ЛФЧХ) разомкнутой системы;
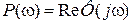- вещественной частотной характеристики замкнутой системы;
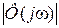- амлитудно-частотный характеристики замкнутой системы.
4. Используя полученные и построенные характеристики, найти и оценить следующие показатели качества системы:
- 
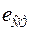- статическую ошибку при подаче на ее входе единичного ступенчатого воздействия;
- частоту среза системы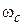 
, запасы устойчивости системы по амплитуде 
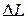и фазе 
;
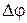- показатель колебательности системы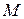 
;
- время регулирования tp и перерегулирование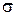 
.
5.Найти дифференциальное уравнение замкнутой системы, связывающее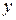 
и 
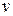(полагая 
).
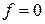6. Найти уравнения состояния замкнутой системы в векторно-мат-ричном виде, в нормальной форме, связывающие координаты 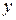и 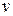(полагая ).
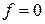Методические указания
1.Передаточные функции находятся с использованием правил структурных преобразований [1, с. 27-34].
2.Если найдена главная передаточная функция замкнутой системы в виде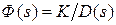 
, где K = K 1 K 2 K 3 − общий коэффициент передачи прямой цепи, 
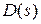− полином относительно 
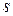, то характеристическое уравнение замкнутой системы имеет вид:
.
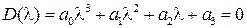Коэффициенты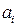 
зависят от параметров системы 
, 
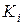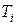. Условие устойчивости в соответствии с критерием Гурвица для системы третьего порядка имеет вид: 
, 
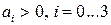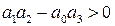. При заданных 
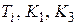из полученных условий устойчивости определяется ограничение на величину коэффициента передачи 
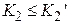далее принимается 
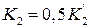[1, c. 47-50].
3. Определение частотных характеристик и их построение подробно изложены в [1, c. 17, 34]. АФЧХ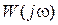 
строится на комплексной плоскости. Ось абсцисс − действительная (
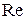), а ось ординат − мнимая (
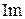). Частота изменяется от 
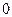до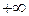 
. Все остальные характеристики имеют ось абсцисс, на которой откладывается частота 
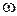(для ЛАЧХ и АФЧХ в логарифмическом масштабе) и соответствующую ось ординат (это модуль или фаза).
Все частотные характеристики строятся обычным способом. Задавая величину 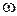дискретно: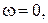 
, 
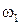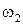,..., находят соответствующее значение ординаты и по точкам строят характеристику. ЛАЧХ 
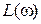обычно строится в виде асимптотической характеристики, состоящей из отрезков прямых.
4. Статическая ошибка определяется по формул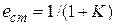е 
, где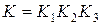 
. Частота среза 
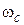определяется по графику ЛАЧХ. Это значение частоты, при котором 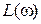пересекает ось абсцисс и где 
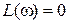. Запасы устойчивост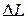и и 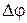также находятся из логарифмических характеристик [1, с. 56]. Показатель колебательности определяют из графика амплитудно-частотной характеристики замкнутой системы 
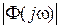, как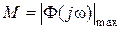 
. Время регулирования 
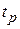и перерегулирование 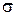ориентировочно можно оценить, используя максимальное значение P max вещественной частотной характеристики 
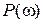и частоту среза .
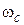Графики, связывающие 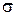, , 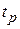P max и 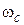представлены в [1, с. 78].
5. Зная передаточную функцию, связывающую изображения входа и выхода системы, нетрудно получить дифференциальное уравнение, связывающее входную и выходную координаты системы [1, c. 33].
6. По дифференциальному уравнению, найденному в предыдущем пункте, легко найти уравнения состояния в нормальной форме [1, с. 90].
