КАФЕДРА ФИЗИКИ
Лабораторная работа.
Вынужденные колебания и явление резонанса в колебательном контуре.
Выполнил: Бороухин А. П.
Принял: Федоров М. И.
ВОЛОГДА 2001г.
Вынужденные колебания и явление резонанса в колебательном контуре.
Оборудование: звуковой генератор, ламповый вольтметр, миллиамперметр, магазин ёмкостей, магазин индуктивности, магазин сопротивлений.
Цель работы: экспериментальное получение резонансных кривых электрического контура, исследование зависимости положения и формы резонансной кривой от параметров контура, исследование связи формы резонансной кривой и добротности электрического контура.
КРАТКАЯ ТЕОРИЯ
При включении в колебательный контур источника переменного тока в контуре происходят вынужденные колебания с частотой 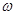 . Учитывая переменную Э.Д.С. и выразив
. Учитывая переменную Э.Д.С. и выразив  через
через 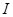 ,получим:
,получим:
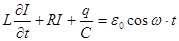 (1)
(1)
где 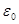 -амплитуда Э.Д.С.,
-амплитуда Э.Д.С., 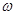 –частота, L-индуктивность.
–частота, L-индуктивность.
Решением уравнения (1) будет:
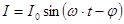 (2)
(2)
где 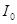 – амплитуда тока в контуре,
– амплитуда тока в контуре, 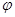 - сдвиг фаз между током и напряжением.
- сдвиг фаз между током и напряжением.
Величины 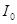 и
и 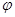 определяются формулами:
определяются формулами:
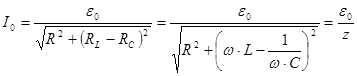 (3)
(3)
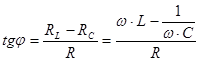 (4)
(4)
где 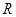 – омическое (активное) сопротивление контура,
– омическое (активное) сопротивление контура,
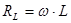 - индуктивное сопротивление контура,
- индуктивное сопротивление контура,
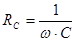 - ёмкостное сопротивление контура.
- ёмкостное сопротивление контура.
Величина 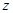 называется полным сопротивлением контура:
называется полным сопротивлением контура:
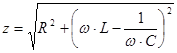 (5)
(5)
При некотором значении частоты
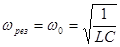 (6)
(6)
Определяемой из условия:
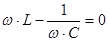 (7)
(7)
Полное сопротивление контура становиться минимальным и равным активному сопротивлению (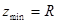 ). При этом амплитуда тока достигает максимума, а сдвиг фаз становиться равным нулю (
). При этом амплитуда тока достигает максимума, а сдвиг фаз становиться равным нулю (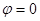 ).
).
Контур действует как активное сопротивление. Такой случай вынужденных колебаний называют резонансом напряжений. При резонансе напряжений на индуктивности 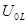 и на ёмкости
и на ёмкости 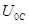 определяется формулами:
определяется формулами:
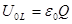 и
и 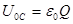 (8)
(8)
Если переменный ток синусоидальный, то
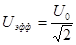 ,
, 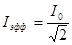 (9)
(9)
Выразив 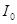 и
и 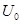 из уравнения (9) и подставив в уравнение (8), получим:
из уравнения (9) и подставив в уравнение (8), получим:
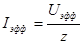 (10)
(10)
Для участков содержащих только один из элементов 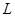 и
и 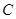 , полное сопротивление определяется соответственно уравнениями:
, полное сопротивление определяется соответственно уравнениями:
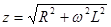 (11)
(11)
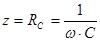 (12)
(12)
Отсюда следует, что измерив величины J и U на индуктивности или эмкости, с помощью уравнений (11) и (12) можно найти величины L и C.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Таблица №1 (C1,L1):
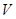 , Гц , Гц
| 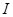 , мА , мА
| 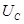 , В , В
|  , В , В
| 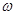 , Гц , Гц
|
| 4,60 | 3,65 | 2,00 | ||
| 5,50 | 3,85 | 1,90 | ||
| 6,40 | 4,15 | 1,80 | ||
| 6,60 | 3,90 | 1,68 | ||
| 6,80 | 3,60 | 1,68 | ||
| 6,47 | 3,40 | 1,70 | ||
| 6,00 | 3,05 | 1,74 | ||
| 5,60 | 2,66 | 1,78 | ||
| 5,15 | 2,35 | 1,80 | ||
| 4,70 | 2,04 | 1,83 |
Таблица №2 (C2,L2):
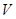 , Гц , Гц
| 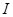 , мА , мА
| 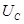 , В , В
| 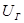 , В , В
| 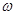 , Гц , Гц
|
| 1,60 | 2,22 | 2,17 | ||
| 2,95 | 2,32 | 2,15 | ||
| 4,90 | 2,58 | 2,05 | ||
| 7,35 | 2,90 | 1,85 | ||
| 10,00 | 3,25 | 1,50 | ||
| 11,00 | 2,80 | 1,22 | ||
| 5,85 | 0,85 | 1,90 | ||
| 4,15 | 0,48 | 2,02 | ||
| 3,25 | 0,32 | 2,10 | ||
| 2,60 | 0,24 | 2,12 | ||
| 2,15 | 0,20 | 2,13 | ||
| 1,85 | 0,18 | 2,15 | ||
| 1,68 | 0,18 | 2,18 |
График к Таблице №1:
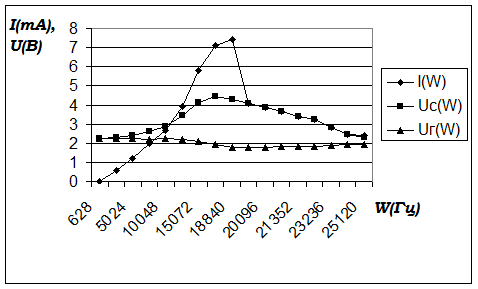 |
График к Таблице №2:
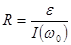
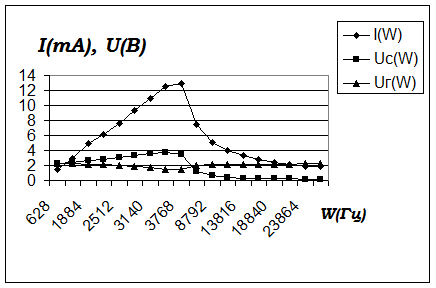 |
;
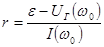 ;
; 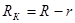 ;
;
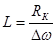 ;
; 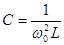 ;
; 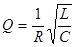 ;
; 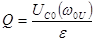 .
.
 2015-06-14
2015-06-14 496
496







