В настоящее время нет общей теории, которая достаточно корректно описывала бы все виды адсорбции на различных адсорбентах и разных поверхностях раздела фаз. Широкое применение нашла теория Ленгмюра о мономолекулярном слое. В основе её лежат следующие положения:
1. Адсорбция является локализованной и вызывается силами, близкими к химическим.
2. Адсорбция молекул адсорбата происходит на активных центрах, каковыми являются пики, ребра, возвышения, имеющиеся на любой поверхности.
3. Активные центры характеризуются большой ненасыщенностью силового поля, что позволяет им удерживать молекулы адсорбата.
4. Каждый активный центр обладает мальм радиусом действия и способен насыщаться. Поэтому активный центр может провзаимодействовать только с одной молекулой адсорбата. В результате на поверхности адсорбента образуется только один слой адсорбата (мономолекулярный слой)
5. Адсорбированные молекулы удерживаются данным активным центром в течение определенного времени, после чего отрываются от активного центра, а он адсорбирует новые молекулы. 
6. Силы взаимодействия между адсорбированными молекулами не учитываются.
На основании приведенных положений было выведено уравнение изотермы локализованной адсорбции
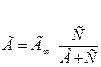
Где:
С - равновесная концентрация,
А - константа адсорбционного равновесия (отношение скоростей десорбции и адсорбции),
Г∞- предельная адсорбция.
Из уравнения следует, что:
1) при малых концентрациях (С «А) адсорбция пропорциональна концентрации,
что соответствует первому участку (I) изотермы адсорбции и отвечает относительно свободной поверхности адсорбента.
2) при высоких концентрациях (С» А) адсорбция стремится к предельному значению, т.е. величина адсорбции не зависит от концентрации. На изотерме это прослеживается на третьем участке (III), когда поверхность адсорбента полностью заполнена.
Константы в уравнении Ленгмюра находятся графическим методом, для чего исходное уравнение приводится к виду уравнения прямой:
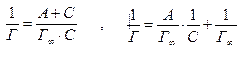
Зависимость между 1/Г и 1/С (рис. 3) характеризуется прямой линией, тангенс
угла наклона которой равен А/ Г∞, а отрезок, отсекаемый на оси ординат, равен 1/ Г∞.
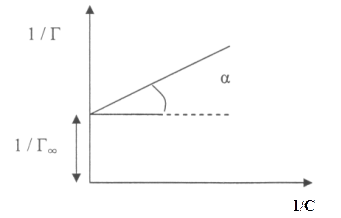
Рис. 3 Графическое определение коэффициентов А и Г∞ уравнения Ленгмюра
Используя представления Ленгмюра о предельной величине адсорбции, можно рассчитать площадь поперечного сечения молекулы. Предельная адсорбция (Г∞) численно равна избыточному количеству вещества (моль), приходящемуся на единицу поверхности (м2). Произведение предельной адсорбции на постоянную Авогадро (Г∞ · Na) определяет число молекул, которое занимает единицу площади. Из этого следует, что площадь поперечного сечения молекулы в насыщенном адсорбционном слое можно рассчитать по уравнению
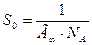

Уравнение Ленгмюра пригодно как для описания адсорбции растворенных веществ, так и для адсорбции газов. В последнем случае концентрацию заменяют пропорциональной величиной - давлением газа.
Наряду с мономолекулярной может наблюдаться полимолекулярная адсорбция, которая описывается теорией Поляни (1915 г). Брунауэр, Эммет и Теллер (1935 - 1940 г.) попытались обобщить представления Ленгмюра и Поляни и описать изотермы адсорбции различной формы с помощью одного уравнения (Теория БЭТ).
 2015-06-14
2015-06-14 601
601








