Средние и предельные ошибки выборки

После проведения отбора для определения возможных границ генеральных характеристик рассчитывается средняя (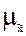) и предельная ошибка выборки (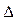), которые связаны между собой следующим соотношением:

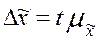
где t – коэффициент доверия, определяющий уровень вероятности при котором выполняется данное равенство.

Приведем наиболее часто употребляемые уровни доверительной вероятности и соответствующие значения для выборок достаточно большого объема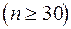

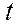
	10,0	1,96	2,00	2,58	3,00
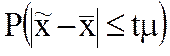
	0,683	0,950	0,954	0,990	0,997

В математической статистике доказывается, что величина средней квадратической стандартной ошибки простой случайной повторной выборки может быть определена по формуле:

.

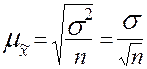Следовательно, чем больше вариация признака, тем больше ошибка выборки и чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик.

Величину 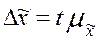называют предельной ошибкой выборки. Она равна 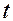-кратному числу средних ошибок выборки. Допустим, что 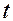= 2. Тогда, 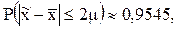т.е. с вероятностью, равной 0,9545, можно ожидать, что ошибка выборочной средней не превысит удвоенной средней квадратической ошибки выборки. Таким образом, величина предельной ошибки выборки может быть установлена с определенной вероятностью.

Средняя квадратическая ошибка случайной бесповторной выборки определяется по формуле

.

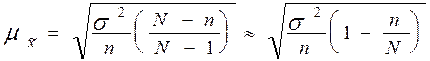Выборочное наблюдение проводится в целях распространения выводов, полученных по данным выборки, на генеральную совокупность. Одной из основных задач является оценка по данным выборки интересующих нас характеристик (параметров) генеральной совокупности.

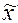- средняя арифметическая выборочной совокупности

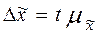, - предельная ошибка этой средней, которая показывает (с определенной вероятностью), насколько выборочная средняя может отличаться от генеральной средней в большую или меньшую сторону. Тогда величина генеральной средней будет представлена интервальной оценкой, для которой нижняя граница будет равна 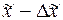, а верхняя граница 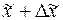. Пределы, в которых с данной степенью вероятности будет заключена неизвестная величина оцениваемого параметра, называют доверительными, а вероятность Р - доверительной вероятностью.

Доверительный интервал для генеральной средней можно записать как:

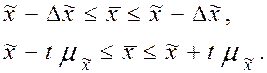
Пример 1: