Формулы по теме: выборочное наблюдение

Средняя ошибка выборки:

повторный отбор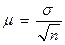

бесповторный отбор ,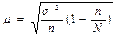

где: s² - выборочная (или генеральная) дисперсия;

s - выборочное или генеральное среднее квадратическое отклонение;

n - объем выборочной совокупности;

N - объем генеральной совокупности.

Предельная ошибки выборки:

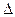= tm,

где: - предельная ошибка выборки;

m - средняя ошибка выборки;

t - коэффициент доверия, определяемый в зависимости от уровня вероятности.

Некоторые значения t и Р:

Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности.

Например, для выборочной средней такие пределы устанавливаются на основе следующих соотношений:

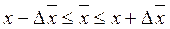
где: х и х - генеральная и выборочная средняя соответственно;

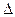х - предельная ошибка выборочной средней.