Мода представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой.
Медиана – это значение признака, приходящееся на середину упорядоченной совокупности.
Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от нее меньше, чем от любой другой величины.
Вычислене моды и медианы зависит от того, какими данными мы располагаем: несгрупированными или сгруппированными.
Мода, в отличие от средней арифмитической, не зависит от минимального и максимального значения ряда распределения.
Медиана практически выполняет функции средней для неоднородной совокупности, а также в тех случаях, когда имеют случаи резкие различия междй максимальным и минимальным значением изучаемого признака.
При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле:
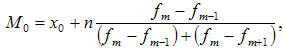
где:
§ 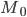 — значение моды
— значение моды
§ 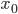 — нижняя граница модального интервала
— нижняя граница модального интервала
§ 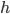 — величина интервала
— величина интервала
§ 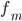 — частота модального интервала
— частота модального интервала
§ 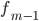 — частота интервала, предшествующего модальному
— частота интервала, предшествующего модальному
§ 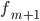 — частота интервала, следующего за модальным
— частота интервала, следующего за модальным
При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:
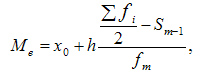
где:
§ 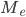 — искомая медиана
— искомая медиана
§ 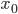 — нижняя граница интервала, который содержит медиану
— нижняя граница интервала, который содержит медиану
§ 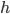 — величина интервала
— величина интервала
§ 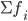 — сумма частот или число членов ряда
— сумма частот или число членов ряда
§ 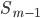 - сумма накопленных частот интервалов, предшествующих медианному
- сумма накопленных частот интервалов, предшествующих медианному
§ 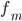 — частота медианного интервала
— частота медианного интервала
 2015-06-04
2015-06-04 882
882








