Решение задач
Задача 1.
Найдите значения других трёх основных тригонометрических функций.
Варианты задания представлены в Таблице №4.
| Таблица №4 | ||
| № варианта | Значение функции | Угол |
| Cos α = -0,8 | π<α<3π/2 | |
Sin α = 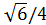
| π/2<α<π | |
Sin α = 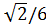
| 0<α<π/2 | |
| Cos α = 15/17 | 3π/2<α<2π | |
| Cos α = -0,7 | π<α<3π/2 | |
Sin α = 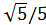
| π/2<α<π | |
Sin α = 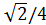
| 0<α<π/2 | |
| Cos α = 14/17 | 3π/2<α<2π | |
| Cos α = -0,6 | π<α<3π/2 | |
Sin α = 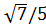
| π/2<α<π | |
Sin α = 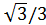
| 0<α<π/2 | |
| Cos α = 16/17 | 3π/2<α<2π | |
| Cos α = -0,9 | π<α<3π/2 | |
Sin α = 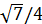
| π/2<α<π | |
Sin α = 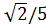
| 0<α<π/2 | |
| Cos α = 12/17 | 3π/2<α<2π | |
| Cos α = -0,5 | π<α<3π/2 | |
Sin α = 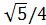
| π/2<α<π | |
Sin α = 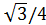
| 0<α<π/2 | |
| Cos α = 13/17 | 3π/2<α<2π | |
| Cos α = -0,4 | π<α<3π/2 | |
Sin α = 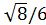
| π/2<α<π | |
Sin α = 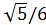
| 0<α<π/2 | |
| Cos α = 11/17 | 3π/2<α<2π | |
| Cos α = -0,3 | π<α<3π/2 | |
Sin α = 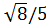
| π/2<α<π | |
Sin α = 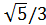
| 0<α<π/2 | |
| Cos α = 10/17 | 3π/2<α<2π | |
Sin α = 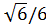
| π/2<α<π | |
Sin α = 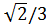
| 0<α<π/2 |
Задача 2.
Найдите область определения и область значений функций. Постройте их графики. Определите, какие преобразования были проделаны с данными графиками.
Варианты задания представлены в Таблице №5.
| Таблица №5 | ||
| № варианта | Функция 1 | Функция 2 |
| Y=2+sin x | Y=1,5 - sin x | |
| Y=cos x-1 | Y=2+cos x | |
| Y=2 - sin x | Y=sin x-1 | |
| Y=0,5+ tg x | Y= tg x-1 | |
| Y= - 0,5+tg x | Y=1+tg x | |
| Y=3+sin x | Y=3 - sin x | |
| Y=0,5 - cos x | Y= cos x-0,5 | |
| Y= - 1,5+ sin x | Y=sin x-1,5 | |
| Y=sin x-2 | Y=sin x+1,5 | |
| Y=sin x-2,5 | Y= - sin x+4 | |
| Y=sin x-3 | Y=sin x +5 | |
| Y=sin x-3,5 | Y=sinx+4 | |
| Y=cos x-2 | Y=cos x+3 | |
| Y=cos x-2,5 | Y= - cos x+2 | |
| Y=cos x-3 | Y= - cos x+1,5 | |
| Y=cos x-3,5 | Y= - cosх+4 | |
| Y= - 1,5+ tg x | Y=tg x-1,5 | |
| Y=tg x-2 | Y= - tg x+2 | |
| Y=tg x-2,5 | Y=tg x+1,5 | |
| Y=tg x-3 | Y= - tg x+3 | |
| Y=1,5 - ctg x | Y=tg x+1,5 | |
| Y=ctg x-2 | Y=2 - ctg x | |
| Y=ctg x-2,5 | Y=3+ctg x | |
| Y=ctg x-3 | Y=0,5+ctg x | |
| Y=2-sin x | Y= - 3+sin x | |
| Y= - cos x-1 | Y= - 2+cos x | |
| Y= - 2- sin x | Y= - sin x-1 | |
| Y= - 2 - tg x | Y= tg x-4 | |
| Y=2+tg x | Y=2+tg x | |
| Y=3-sin x | Y=sin(-2 x) |
Задача 3.
Вычислите значение обратных тригонометрических функций.
Варианты задания представлены в Таблице №6.
| Таблица №6 | |
| № варианта | Задание |
аrcsin (- 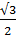 ) + arccos (- ) + arccos (- 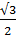 ) + arctg ) + arctg 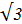
| |
аrcos 1 + 2arcctg (- 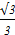 ) )
| |
| аrcsin 1 + arcos 1 + arctg 1 +arcctg 1 | |
аrcsin 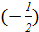 + arcos + arcos 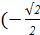 ) + arctg 0 ) + arctg 0
| |
аrcctg 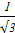 + arcos + arcos 
| |
аrcsin 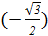 + arctg + arctg 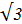
| |
2arcsin 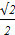 - arcctg - arcctg 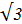
| |
аrcsin 0 + arcsin 1 + 2arcctg (- 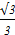 ) )
| |
аrcctg 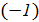 - arcos 1 - arcos 1
| |
arcos 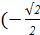 ) +arcctg (-1) ) +arcctg (-1)
| |
аrcsin  - arsin - arsin 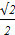
| |
аrcsin (- 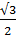 ) + arccos (- ) + arccos (- 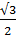 ) +arcctg 1 ) +arcctg 1
| |
2arccos 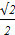 + 2arcctg (- + 2arcctg (- 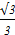 ) )
| |
аrctg 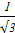 + arcos + arcos 
| |
аrctg 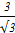 - arcsin - arcsin 
| |
аrcsin 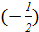 + arcos + arcos 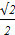 + arctg 1 + arctg 1
| |
аrccos  + arcsin + arcsin 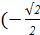 ) + arcctg1 ) + arcctg1
| |
аrcos 0 + arcctg 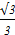
| |
arctg 0 + arccos 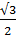 - arcctg 1 - arcctg 1
| |
arcsin 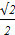 + аrcctg + аrcctg 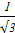
| |
arctg 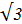 + + arsin + + arsin 
| |
аrcctg 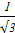 + arcos + arcos 
| |
arccos (- 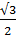 ) + arctg ) + arctg 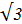
| |
| Таблица №6(продолжение) | |
| № варианта | Задание |
аrcsin 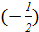 + arcos + arcos 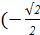 ) )
| |
arcsin 0 + arcctg (- 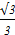 ) )
| |
аrcsin1 + 2arctg 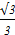
| |
| аrccos 1 + arcsin 0 | |
| arcos 1 + arcctg 0 | |
arccos 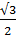 - arcctg (-1) - arcctg (-1)
| |
аrccos 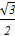 + arcctg + arcctg 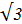
|
Таблица оценивания №4
| Вид самостоятельной работы | Баллы |
| Решение задач | |
| Задача 1 | 3 балла |
| Задача 2 | 5 баллов |
| Задача 3 | 2 балла |
| Итого: | 10 баллов |
 2015-06-04
2015-06-04 606
606








