Свойства. 2. Положительность: Если интегрируемая функция неотрицательна, то её интеграл на отрезке

1. Невырожденность: .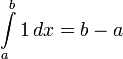

2. Положительность: Если интегрируемая функция 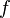неотрицательна, то её интеграл на отрезке 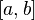также неотрицателен.

3. Линейность: Если функци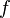и и 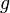интегрируемы, и 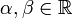, то функция 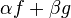тоже интегрируема, и .

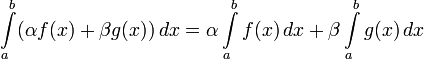4. Непрерывность: Если интегрируемые функции 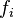равномерно сходятся на отрезке 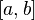к функции 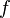, то 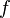интегрируема, и 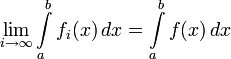. (Последняя формула может быть получена уже как формальное следствие свойств 1-3 и интегрируемости предельной функции).

5. Аддитивность при разбиениях отрезка: Пусть 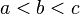. Функция 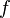интегрируема на отрезке 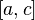, тогда и только тогда, когда она интегрируема на каждом из отрезков 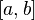и 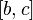, при этом .

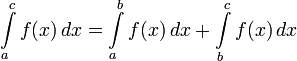6. Непрерывная на отрезке функция интегрируема по Риману (следствие свойств 1-5). Разрывные функции могут быть интегрируемы, но могут и не быть; примером функции, не интегрируемой по Риману, является всюду разрывная функция Дирихле. Критерий Лебега интегрируемости функции по Риману: функция интегрируема по Риману на отрезке 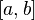, если и только если на этом отрезке она ограничена, и множество точек, где она разрывна, имеет нулевую меру (то есть может быть покрыто счётным семейством интервалов со сколь угодно малой суммарной длиной).

7. Если функция 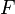является первообразной непрерывной функции 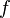, то интеграл функции 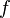на отрезке 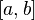может быть вычислен по формуле Ньютона-Лейбница: он равен 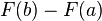. (Это — общее свойство любых интегралов, удовлетворяющих свойствам 1-5, а не только интеграла Римана). Непрерывная на отрезке функция 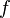всегда имеет первообразную, и каждая первообразная имеет вид: 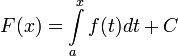, где 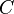— произвольная константа.