Пусть на отрезке 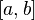 определена вещественнозначная
определена вещественнозначная
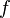 .
. Рассмотрим разбиение отрезка 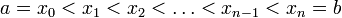 — конечное множество попарно различных точек отрезка. Это разбиение делит отрезок
— конечное множество попарно различных точек отрезка. Это разбиение делит отрезок 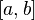 на n отрезков
на n отрезков 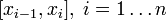 . Длина наибольшего из отрезков
. Длина наибольшего из отрезков 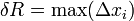 называется шагом разбиения, где
называется шагом разбиения, где 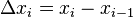 — длина элементарного отрезка.
— длина элементарного отрезка.
Отметим на каждом отрезке разбиения по точке 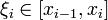 . Интегральной суммой называется выражение
. Интегральной суммой называется выражение 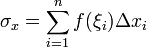 .
.
Если при стремлении шага разбиения к нулю интегральные суммы стремятся к одному и тому же числу, независимо от выбора 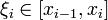 , то это число называется интегралом функции
, то это число называется интегралом функции 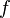 на отрезке
на отрезке 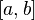 , то есть
, то есть 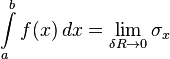 .
.
В этом случае, сама функция 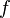 называется интегрируемой (по Риману) на
называется интегрируемой (по Риману) на 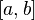 ; в противном случае
; в противном случае 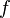 является неинтегрируемой (по Риману) на отрезке
является неинтегрируемой (по Риману) на отрезке 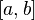 .
.
 2015-06-16
2015-06-16 281
281







